最近のプログラマーは、ライブラリなど便利な道具やツールが豊富に存在しています。検索すればブラウザに答えが表示されます。しかも無料であることも多いです。なんとも素晴らしい環境で開発しています。
私もその恩恵にあやかっている一人ですが、ここでは一旦、基本に立ち返って、コンピュータがどのように計算しているかニュートン近似法について掲載しています。頭の体操になると思います。
スポンサーリンク
ニュートン近似法
方程式 f(x) = 0 の解を近似的に求めることを考えてみます。
x2 – 5 = 0 の解は、±√5 です。
グラフでは次のようになります。プログラマのみなさん、懐かしいですか?
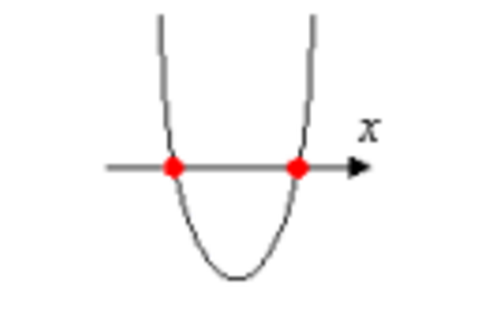
2次関数のグラフ
ニュートン近似法を使って近似値を計算する方法の一つに開平計算という計算法があります。しかし、微分法を使って一般的で計算速度の速い方法がニュートン近似法です。
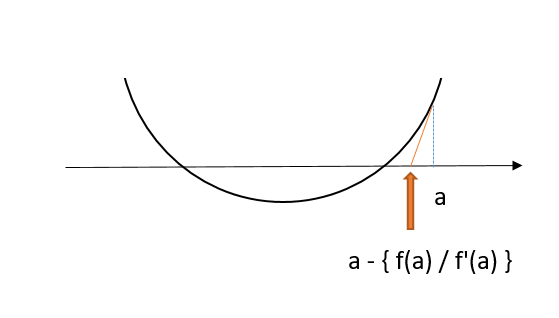
ニュートン近似法
x 座標を仮に a だとすると、⇧ で示した座標は上のグラフの通り、以下の式で表すことができます。
a – { f(a) / f'(a) }
これを、グラフが x 座標と交わる位置までドンドン続けていきます。
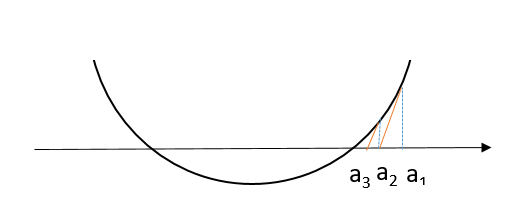
ドンドン続ける
このとき、an+1 と an の関係は次式で表すことができます。
an+1 = an ー { f(an) / f'(an) } = an / 2 + 5 / 2an
√5 ≒ 2.236 であり、2と3の間にある数ということはわかりますので、a1 = 3 から計算していきます。
a1 = 3
a2 = 3 / 2 + 5 / 6 = 7 / 3
a3 = 1 / 2 × 7 / 3 - 5 / (2 × 7 / 3) =47 /21
a4 = ・・(省略)・・= 2207 / 987 ≒ 2.23606
a4 まで計算することで、小数点以下5桁まで間違いなく計算されています。なお、a5、a6 と計算を続けることで、正しく計算される小数点以下の桁数が倍々ゲームで一致していきます。
暇なら計算してみてください
このように、単純な計算で効率よく計算することができるため、コンピュータでの近似値計算に利用されています。多分ですが・・・・
ニュートンは偉大です。計算できる人ってかっこいいですね。