ここでは、ブログタイトルにも含まれる偏差値がどのように考えられ、計算するのかを掲載しています。
バカも天才も正規分布に従い分布しています。なお、バカと天才は紙一重と言いますが、全く違います。
スポンサーリンク
偏差値が必要な理由
同じ難易度の試験問題を作ろうとしても、簡単ではないことは想像しやすいと思います。ある人が受けた異なる試験の結果が同じ60点だったとしても、その60点を比較しても意味がありません。
1回目の試験の平均点が50点、2回目の試験の平均点が70点だった場合を考えてみると意味のないことが分かります。そこで、平均点とバラツキ具合をそろえれば比較可能と考え、偏差値が登場しました。
偏差値の計算方法
偏差値の計算方法は次の通りです。
平均点:m
標準偏差:σ
自分の点数:x
とすると、
偏差値 = 10 × ( x – m ) / σ + 50
プログラムの記事で読みにくいですが、以下のリンクに計算方法を記載しています。よろしければ参照ください。
正規分布
同学年の生徒の身長などの数値のように、あまり偏りのない多くのサンプルの分布は正規分布になることが知られています。ほとんどの生徒が大きい、または小さい身長といった偏っていることがないことはイメージできると思います。
正規分布の中でも、特別なモノが標準正規分布でこれを表にしたものが標準正規分布表です。
標準正規分布表
標準正規分布票は下表のとおりです。なお一部であり、全てではありません。赤字の部分は、別途、後述してあります。
| x | 0.00 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.50000 | 0.49601 | 0.49202 | 0.48803 | 0.48405 | 0.48006 | 0.47608 | 0.47210 | 0.46812 | 0.46414 |
| 0.1 | 0.46017 | 0.45620 | 0.45224 | 0.44828 | 0.44433 | 0.44038 | 0.43644 | 0.43251 | 0.42858 | 0.42465 |
| 0.2 | 0.42074 | 0.41683 | 0.41294 | 0.40905 | 0.40517 | 0.40129 | 0.39743 | 0.39358 | 0.38974 | 0.38591 |
| 0.3 | 0.38209 | 0.37828 | 0.37448 | 0.37070 | 0.36693 | 0.36317 | 0.35942 | 0.35569 | 0.35197 | 0.34827 |
| 0.4 | 0.34458 | 0.34090 | 0.33724 | 0.33360 | 0.32997 | 0.32636 | 0.32276 | 0.31918 | 0.31561 | 0.31207 |
| 0.5 | 0.30854 | 0.30503 | 0.30153 | 0.29806 | 0.29460 | 0.29116 | 0.28774 | 0.28434 | 0.28096 | 0.27760 |
| 0.6 | 0.27425 | 0.27093 | 0.26763 | 0.26435 | 0.26109 | 0.25785 | 0.25463 | 0.25143 | 0.24825 | 0.24510 |
| 0.7 | 0.24196 | 0.23885 | 0.23576 | 0.23270 | 0.22965 | 0.22663 | 0.22363 | 0.22065 | 0.21770 | 0.21476 |
| 0.8 | 0.21186 | 0.20897 | 0.20611 | 0.20327 | 0.20045 | 0.19766 | 0.19489 | 0.19215 | 0.18943 | 0.18673 |
| 0.9 | 0.18406 | 0.18141 | 0.17879 | 0.17619 | 0.17361 | 0.17106 | 0.16853 | 0.16602 | 0.16354 | 0.16109 |
| 1.0 | 0.15866 | 0.15625 | 0.15386 | 0.15151 | 0.14917 | 0.14686 | 0.14457 | 0.14231 | 0.14007 | 0.13786 |
標準正規分布表の読み取り方
標準正規分布表をある学年の生徒の身長を例に読み取ってみます。下のグラフの斜線はとりあえず無視してください。
μ が、0 のときにグラフの山が頂点になり、例えば身長で言えば平均値になります。平均から右に行くほど身長が高く、人数も少なくなっています。左に行くほど身長が低く、また身長が低い人数もすくなくなっています。
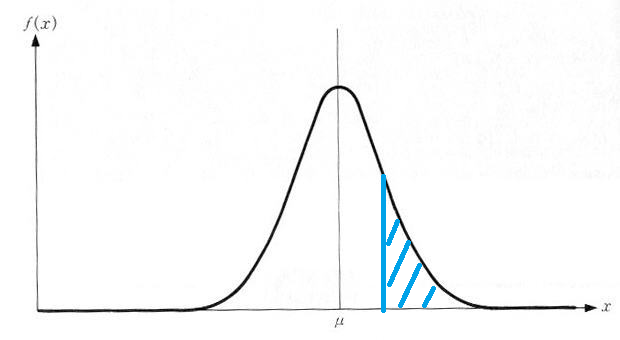
正規分布表
次に、xの計算方法は次のように求めることができます。偏差値と同じような計算方法になります。
x = (自分の身長 ー 身長の平均値) / 標準偏差
次に、仮に自分の身長から x を計算したところ、0.48 になったとします。
つまり、0.48を10倍して50足すと、身長の偏差値が求まります。あまり意味ないですが。
次に、この 0.48 から正規分布票の赤字の値をよみとります。
I(0.48) = 0.31561
なお、I(x) は、上記の正規分布のグラフの斜線の面積になります(全体の面積は1とします)。つまり、xが0.48の人は全体の上から31.5%位の身長であると読み取ることができます。