[ 数ⅢC ] 無限級数（収束 発散）と数列の極限の定理とその証明

ここでは、無限級数の収束と発散と数列の極限に関しての定理とその証明を行っています。

なぜだか、ナメック語を思い出しました。読み書きできませんが。

級数の収束と発散と数列の極限に関する定理

級数 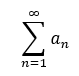の収束、発散と数列｛a_n｝の極限に関しては次の定理が成り立ちます。

定理

証明

②は①の対偶であるので、①を証明してみます。なお、①、②の逆は成り立ちません。注意しましょう。

• （参考）　[ 高校数学 ] 命題と論証 ～ 逆の裏は対偶 ～

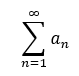の和を S , 第n部分和を S_n とおくと、

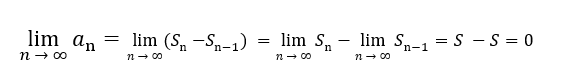
よって、①は成り立ちます。

 

前提知識（無限級数の和）

上記の証明が分からない場合は、次の前提となる知識が不足しているのかもしれません。良い機会ですので覚えておくと良いでしょう。

無限級数 Σ a_n の第 n 項までの和 S_n = Σa_k = a₁ + a₂ + ・・・ + a_n をこの級数の部分和（第n部分和）といいます。

級数 Σa_n の収束、発散は部分和の数列　S₁,  S₂,  S₃,  ・・・ S_n ・・・

の収束、発散により、次のように定義します。