[ 中学数学 ] 周の長さが一定である長方形の面積を最大化する ( 平方完成と導関数 )

ここでは、周の長さがある一定の長さである長方形の面積の最大化について考えてみたいと思います。

問題

20 m のロープで長方形を作ります。このとき面積が最大となるには縦横それぞれ何 m の長方形（正方形）を作ればよいでしょうか？

---

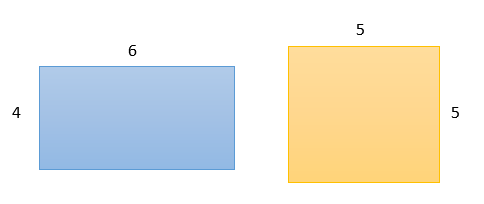
解説

まずは中学生までの知識を使っての解答例です。

周の長さを 2L  とします。縦 + 横 = L となります。縦の長さを a とすると、横の長さは L – a となります。

面積を S とすると、

S = a ( L – a ) であることから

= -a² + La 　・・・① 続いて平方完成です。

= -( a² – La )

= -( a – L / 2 )² + L² / 4

上記は a の 二次方程式 ( 上に凸 ) ですので、面積 S が最大となるのは、( a – L / 2 ) = 0 のときです。

よって L = 2a のとき面積が最大となりますので、縦横が同じ長さの正方形のときに面積は最大値をとることがわかります。

問題の解答は 5 となります。

[ 高校数学 ] 導関数から求める

中学生の解答で何の問題もないですが、高校生になると微分を学びます。文系の方は履修しないかもしれないですね。中学生の方は、雰囲気だけ楽しんでみてください。

なお、グラフはあくまでイメージです。雰囲気だけつかんでください。

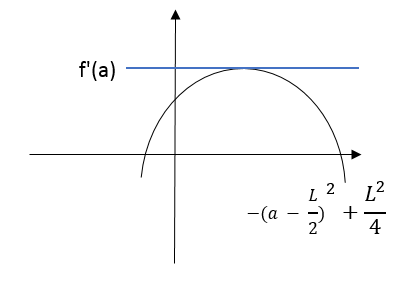
上記で使用した① の式です。

f ( a ) = -a² + La

微分して導関数を求めます。

f ‘ ( a ) = -2a + L

この場合の導関数とは、放物線に接する直線 ( 接線 ) の傾きだと思ってください。

放物線に接する直線の傾きが 0 になるのは、a = L / 2 のときです。またそのときの接線の傾きは 0 ですので、

f ‘ (a) = -2a + L = 0

よって、ここからも、L = 2a の式を導き出すことができました。

四角形全体に拡張する

ここでは結果だけを紹介しておきます。長方形や正方形だけでなく四角形全体で考えると、各辺の長さを一定とするとき、四角形 ABCD の面積を最大化する条件は、

• ∠A + ∠C = 180°　（当然、∠B + ∠D も 180° )

です。長さの違う4本のロープで四角形を作るときに、その面積を最大化する条件です。

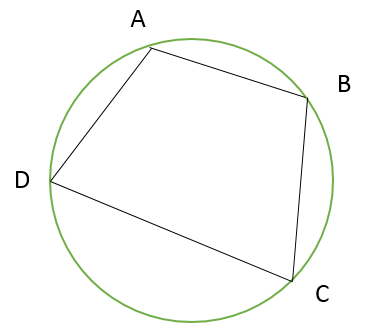
つまり、その四角形は円に内接する四角形であることがわかります。正方形もこの条件に当てはまることからも、イメージしやすいのではないでしょうか。

 

数学は高校入試や大学入試のためにあるわけではありません。最も多くの面積となるように農作地を確保して、米の生産量を最大化するにはどうしたらいいのだろう？などの声が学問のスタート地点です。生活に密着しているのです。