ここでは、sinθ + cosθ と sinθcosθ の関係について説明しています。この関係性を利用した問題も大学入試で出題されることもありますので理解して、覚えておきましょう。
スポンサーリンク
sinθ + cosθ から sinθcosθ を導出する
sinθ + cosθ の値を t とおくと、
t2 = sin2θ + 2sinθ cosθ + cos2θ
ここで、sin2θ + cos2θ = 1 だから
t2 = 1 + 2sinθcosθ
( t2 -1 ) / 2 = sinθcosθ
となるので、
sinθcosθ = { ( sinθ + cosθ )2 -1 } / 2
の関係がわかります。
sin2θ + cos2θ = 1 は、「余角( 90° – θ ) 補角( 180° – θ ) の三角比公式を図で理解する」 で紹介していますので参照ください。
発展
sin3θ + cos3θ と sinθcosθ の関係を利用した問題もよく出題されますので覚えておくと良いでしょう。以下の因数分解の公式があります。
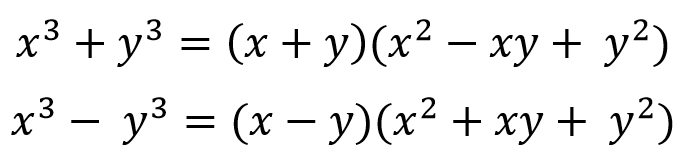
3次式の因数分解公式
この公式から、
sin3θ + cos3θ
= ( sinθ + cosθ ) ( sin2θ − sinθcosθ + cos2θ )
= ( sinθ + cosθ ) ( 1 − sinθ cosθ )
が導くことができます。
また、前述の sinθ + cosθ の値を t とおくと、( t2 – 1 ) / 2 = sinθcosθ の関係から、
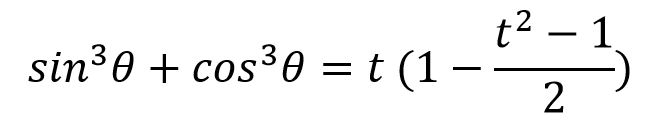
を導出することができます。