[ 高校入試超難問 ] 平成27年 神奈川県数学 問6 の解説

平成27年 神奈川県高校入試 ( 数学 ) の超難問の解説を行っています。ひらめきや発想がポイントだと感じましたが、相当量の訓練がないとひらめくことはできません。

問6

解答・解説

( ア ) 円錐の体積です。円錐の体積は ( 底面積 × 高さ ) / 3 で求めます。

底面積 = 円の面積 = 半径 × 半径 × π = 9 π

高さ ( OC ) は、△AOC が直角三角形なので三平方の定理から求めます。

OC² = AC² – AO² = 10² – 3² = 91
OC = √91 となります。

これらから、円錐の体積は

9π × √91 / 3 = 3π√91 cm³ が求まります。

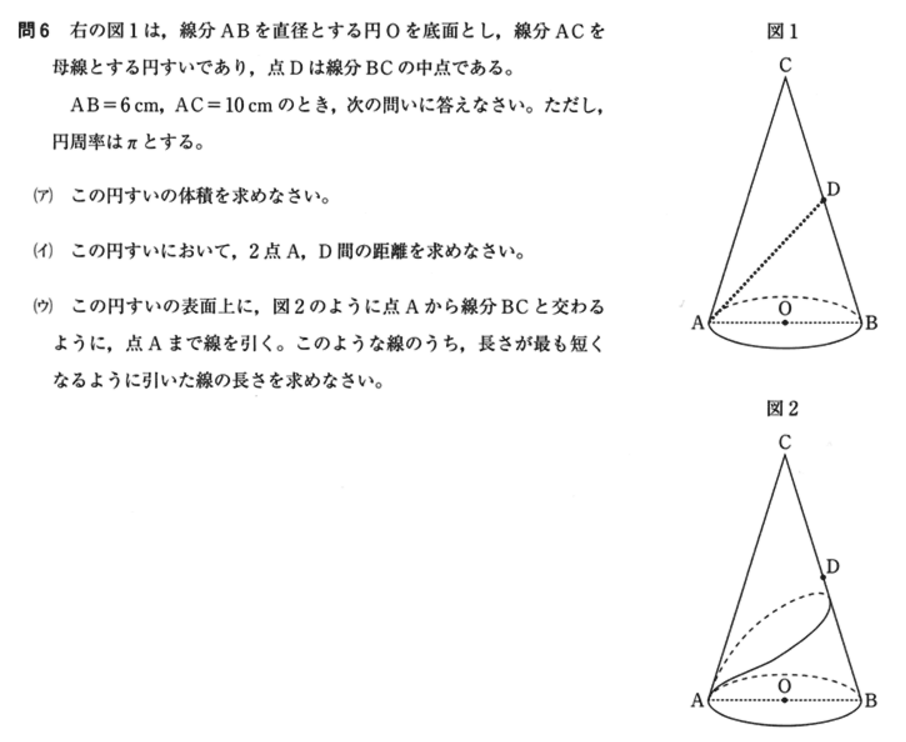
( イ ) AD の長さを求めます。

下の図のように、D から AB に垂線を下ろし、その交点を H とします。また、CO も直線で結びます。

△ BHD と △ BOC は相似であり、D は BC の中点なので相似比は 1 : 2 です。BC = 10 なので、BD = DC = 5 であることがわかります。また、OB = 3 から BH = HO = 3 / 2 であることがわかり、AH = 3 + 3 / 2 = 9 / 2 が求まります。

また、CO = √91 であることから、DH = √91 / 2 です。

△ADH は直角三角形なので、三平方の定理より、

AD² = AH² – DH² = ( 9 / 2 )² – (√91 / 2 )² となり、ADを計算すると

AD = √43 が求まります。

( ウ ) 最も短くなる線は展開図を書くとすぐにわかります。また、この種の類似問題は良く見かけるでしょう。

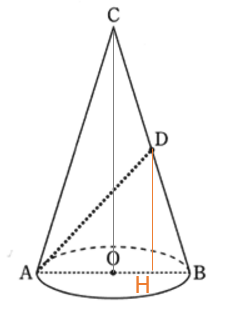
A と A’ は本来同じ点ですが、区別するために一方を A’ としています。最も短いのは直線のときですので、直線 AA’ の長さを求めることになります。

弧AA’ の長さ = 底面の円周 = 6 π

点C を頂点とする半径 CA の円の円周 = 20 π

よって、扇形の中心角度 = ∠ACA’ = 360 × ( 6 / 20 ) = 108°

が求まります。角度が90° であれば簡単に AA’ は求まりそうですが、108° と中途半端です。よって難問確定です。ここからは日ごろの訓練 ( 学習 ) 量が多いほどひらめきます。108° を如何に都合の良い数字だと思うことができる人はそうとうな学習を行っているのではないでしょうか。

下の図のように、∠ACA’ が36° と 76° になるように補助線を引きます。また、AA’ との交点を P とします。

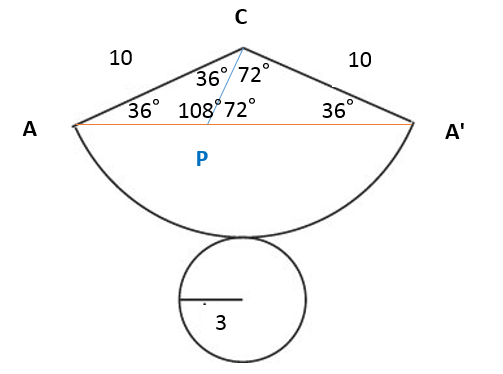
△ACA’ はAC = A’C の二等辺三角形なので、∠CAA’ = ∠CA’A = 36° です。△ACP は36° なので、∠CPA は 108° であるから、△PAC と △ CAA’ は相似であることがわかります。

また、△CPA’ において、∠ PCA’ = ∠CPA’ = 72° であることから、△CPA’ は二等辺三角形であることがわかり、CA’ = A’P = 10 であることもわかります。

AA’ = a とおくと、AP = a – 10

△PAC ∽ △ CAA’ より、

AC : AA’ = AP : AC = 10 : a = ( a – 10 ) : 10

a ( a – 10 ) = 10 × 10

を a について解きます。a についての二次方程式なので a は 2つ求まりますが、

a > 0 なので、

AA’ = a = 5 + 5√5  cm となります。