ここでは、平成28年 ( 2016年 ) 東京都 高校入試 数学 の解説を行っています。
スポンサーリンク
問1

解答・解説
[ 問1 ] -6 – 42 × ( 1 / 8 )
= -6 -16 × ( 1 / 8 )
= -6 – 2 = -8
[ 問2 ] 7a – b -5 ( a – 2b )
= 7a – b -5a + 10b
= 2a + 9b
[ 問3 ] √48 + ( 9 / √3 )
= 4√3 + ( 9√3 / 3 )
= 4√3 + 3√3
= 7√3
[ 問4 ] x + 6 = 2( x + 1 )
x + 6 = 2x + 2
x = 4
[ 問5 ]
9x – 5y = -7 ・・・①
-3x + 2y = 4 ・・・②
① + ② × 3
9x – 5y = -7
-9x + 6y = 12
y = 5
① に y = 5 を代入して
9x -5 × 5 = -7
9x -25 = -7
9x = 18
x = 2, y = 5
[ 問6 ]
x2 + 5x – 6 = 0
( x + 6 ) ( x – 1 ) = 0
x = -6, 1
[ 問7 ]
48分の記録を含む度数 : 12
全員の人数 : 50
相対度数 = 12 / 50 = 0.24
[ 問8 ]
OC を結ぶと △OBC は OB = OC の二等辺三角形、△OCD は OC = OD の二等辺三角形であることから、∠BOD = 160° であることがわかります。
さらに、円周角の定理より x = ∠BAD = 80° であることがわかります。
[ 問9 ] P から ℓ に垂線をひきます。交点を中心に交点と点P の長さを半径とする円を作図します。
問2
解答・解説
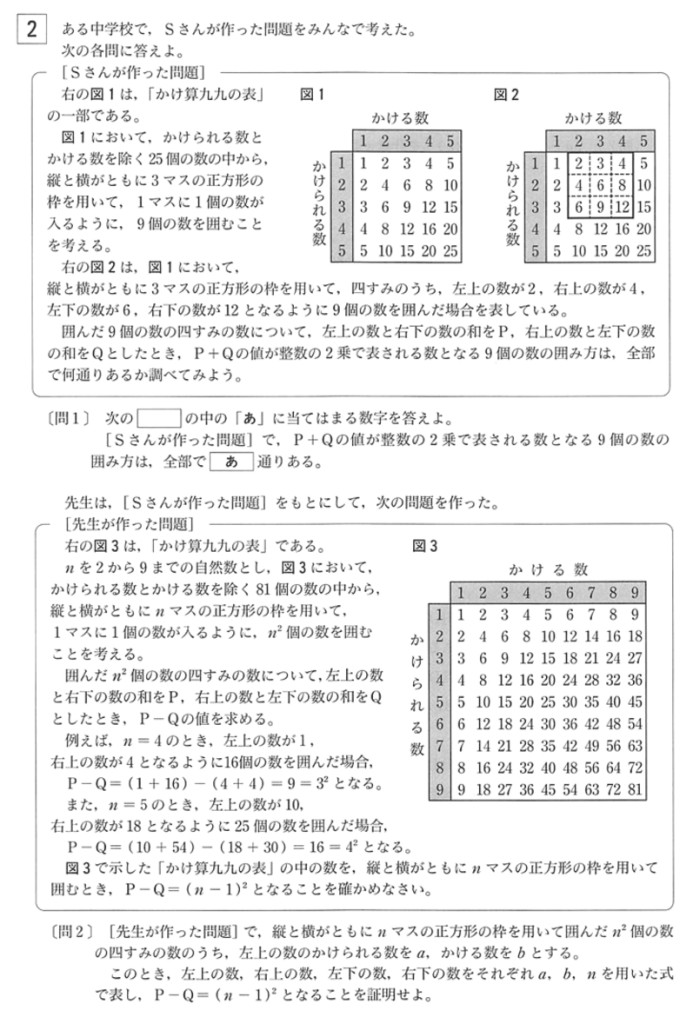
[ 問1 ] P + Q が n の2乗になるようなパターンを探す問題です。
P + Q とありますが、結局のところは4隅の数の合計のことです。n の2乗になるものを探すと下の図のように3通り見るけることが出来ます。
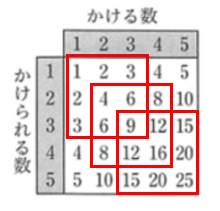
1 + 3 + 3 + 9 = 16 = 42
4 + 8 + 8 + 16 = 36 = 62
9 + 15 + 15 + 25 = 64 = 82
よって、3通り。
[ 問2 ]
a, b, n を用いて4隅の数を表します。
| 数の位置 | 数 |
|---|---|
| 左上 | ab |
| 右上 | a ( b + ( n – 1) ) |
| 左下 | b ( a + ( n – 1 ) ) |
| 右下 | ( a + ( n – 1 ) ) ( b + ( n – 1 ) ) |
次に n – 1 = N といて、P – Q を求めます。がんばって計算してみてください。ここでは結果のみの紹介です。
P – Q = N2 となります。
n – 1 = N なので、
P – Q = ( n – 1 )2 が証明されました。
問題文から計算結果を予想できるようになると理想的です
問3
解答・解説
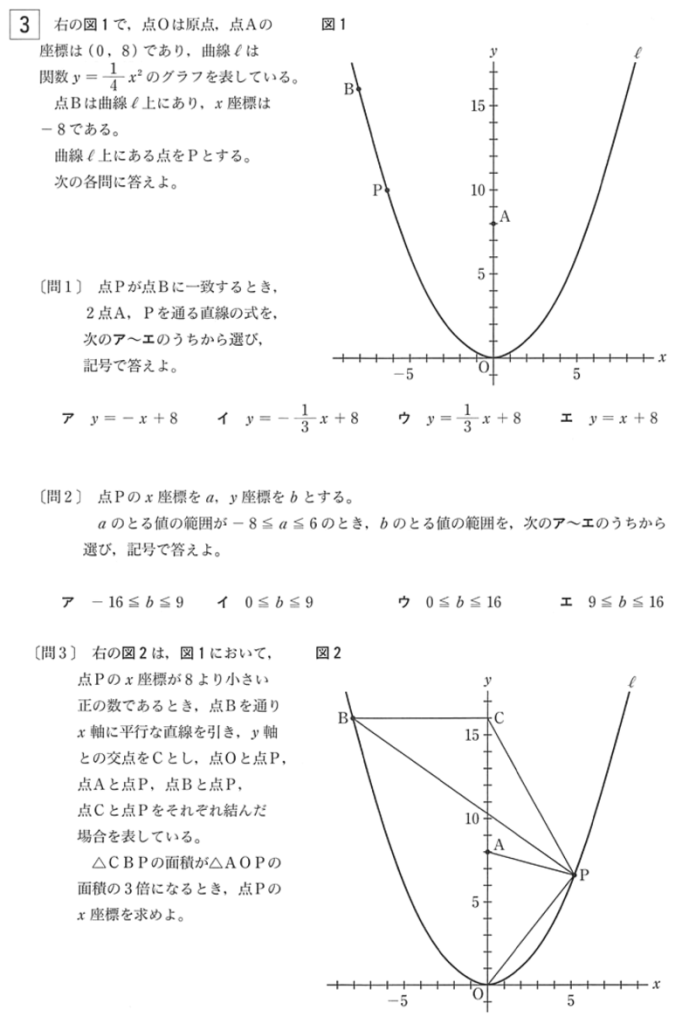
[ 問1 ] 点A ( 0, 8 ) であり、B は曲線上にあり x 座標が -8 なので、y 座標を求めると、点B ( -8, 16 ) がわかります。
よって、2点A, B を通す直線の方程式を求めればよいので、
AB : y = -x + 8 となります。
[ 問2 ] 曲線 ℓ は、下に凸の2次関数であり、x = 0 のとき、y は 最小値 0 となります。また、原点からの距離が長いほど y 座標の値は大きくなるので、x = -8 のとき、y は最大となり y = ( 1/ 4 ) × ( -8 ) × ( -8 ) = 16 となります。
よって、求める答えは 0 ≦ b ≦ 16 となります。
[ 問3 ] 底辺をAO とする △AOP と底辺をBC とする △CBP を考えます。
AO = BC = 8 であることはわかっていますので、残りは高さを考えます。
点P ( t, t2 / 4 ) とおくと、△AOP の高さは t , △BCP の高さは ( 16 – ( t2 / 4 ) ) あらわすことが出来ます。
△BCP の面積が △AOP の面積の3倍なので、以下の方程式が成り立ちます。
( 8 × ( 16 – ( t2 / 4 ) ) ) / 2 = 3 × ( 8 × t / 2 )
t について解くと、
( t – 4 ) ( t + 12 ) = 0 となります。t > 0 なので、
t = 4 となります。
問4

解答・解説
[ 問1 ] まずは与えられた角度を図に書き込んで見ます。
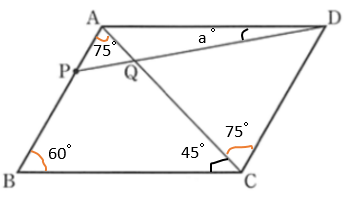
∠ABC = 60° であることから、∠BCD および ∠PAD は 180 – 60 = 120° であることがわかるので、
∠BCA = 45° です。
∠BAC と ∠ACD は錯角で等しいことから 75° とわかります。
△PAD において、∠APD = 180 – 120 – a = ( 60 – a )° です。
△APQ において、∠AQP = 180 – ( 75 + 60 – a ) = ( 45 + a )° となり、対頂角は等しいので
∠CQD = ( 45 + a )° となります。
[ 問2 ] ①
△AQR と △CQP において、
∠AQR = ∠CQR ( 対頂角 ) ・・・①
AS と PC は平行なので
∠ARQ = ∠CPQ ( 平行線の錯角 ) ・・・②
①、②より、2組の角がそれぞれ等しいから
△AQR ∽ △CQP
[ 問2 ] ②
図を再掲載します。
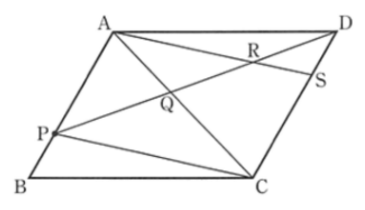
△APQ と △CDQ は相似です。相似比は 2 : 3 です。
よって、AQ : QC = 2 : 3 であることがわかります。
また、問題① より、△AQR ∽ △CQP であるので、△AQR と △CQP 相似比が 2 : 3 であることがわかりました。
面積比は 4 : 9 となります。
次に AC を底辺とする △ACP に着目します。AQ : QC = 2 : 3 なので、
△AQP と △QCP の面積比は 2 : 3 です。△CQP の面積を 9 とすると、△AQP の面積は 6 となります。
△APC と △ACS の面積は等しいので、
△AQP + △QCP = △AQR + 四角形QRSC となります。
6 + 9 = 4 + 四角形QRSC
四角形QRSC の面積 = 11 となります。
四角形APCS の面積 : △AQR の面積 = ( 6 + 9 + 4 + 11 = ) 30 : 4 となり、
求める答えは、4 / 30 = 2 / 15 となります。
問5
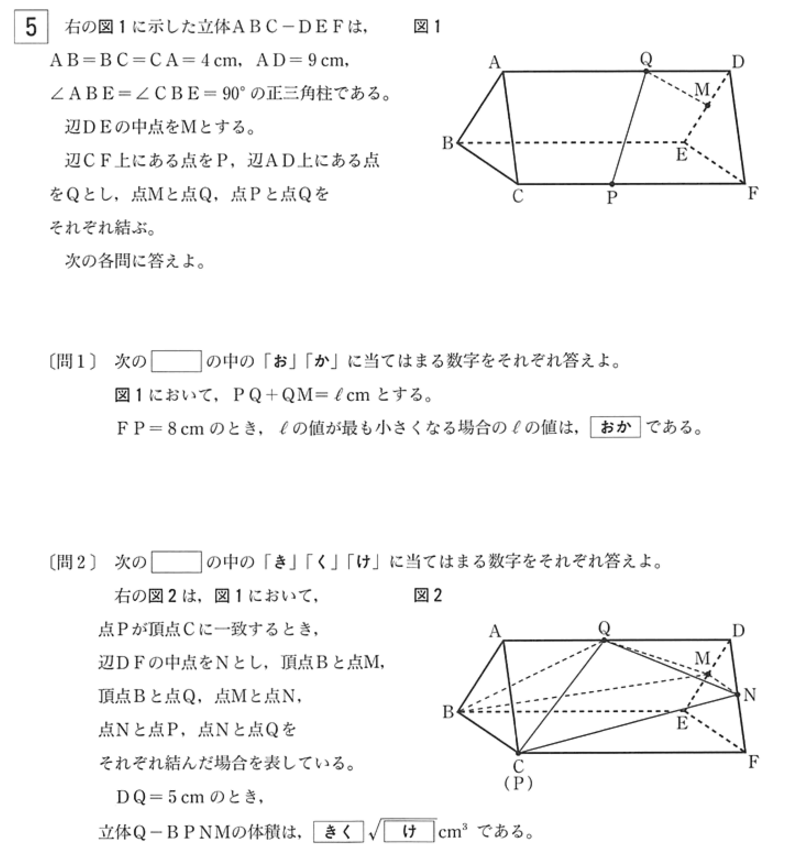
解答・解説
[ 問1 ] 問題文から、求める ℓ は以下の展開図のようになります。
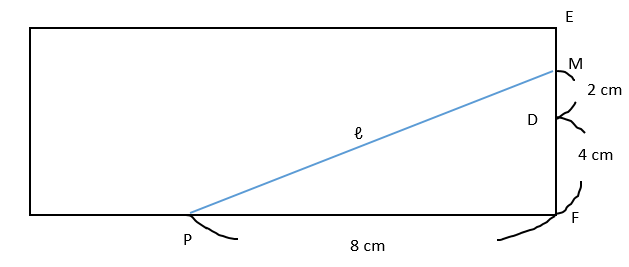
この図から ℓ を三平方の定理を使って求めると、
ℓ2 = PF2 + FM2 = 82 + 62 = 100
よって、ℓ = 10 cm となります。
[ 問2 ]
立体Q-BPMN は四角錐です。また、四角形BPMN は台形です。
BC の中点と EF の中点をそれぞれ R, S とおきます。そのときの、四角形ARSD に着目します。
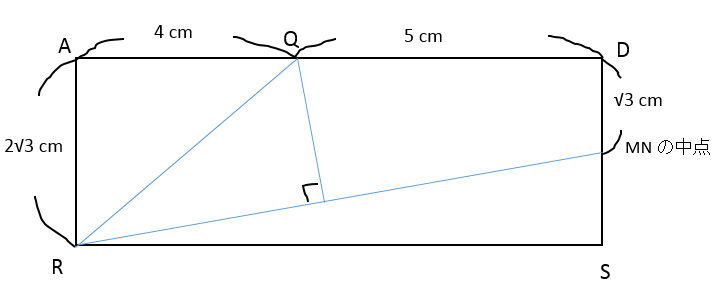
ここから、QR 、R と MN の中点、Q から R と MN の中点に下ろした垂線の距離を三平方の定理を使ってそれぞれ求めます。
頑張って計算してみましょう。また、AR が 2√3 になる理由がわからない場合は、三平方の定理の再学習が必要です。
R と MN の中点 : 2√21 cm
Q から下ろした垂線の長さ : √7 cm
と計算できます。
台形BPMN の面積は ( ( 2 + 4 ) × 2√21 ) / 2 = 6√21 cm2 となりますので、
求める立体Q-BPMN の体積は、
( 6√21 × √7 ) / 3 = 14√3 cm3 です。
一番最後の問題なのですがrとmnの中点を結んだ線分にqの垂線が交わるのは正三角形(二等辺三角形)のていへんを二等分する直線は頂角を二等分して底辺に垂直であるという定義(頂角の二等分線は底辺を垂直に二等分する)を使ったものなのでしょうか(・・?l