平成28年 ( 2016年 ) 神奈川県 高校入試 数学の解説を行っています。
スポンサーリンク
問1
解答・解説
( ア ) -12 + 3 = -9
( イ ) ( 3 / 4 ) – ( 8 / 9 ) = ( 27 – 32 ) / 36 = -5 / 36
( ウ ) 28a2b2 ÷ 4ab2 = 7a
( エ ) ( 8 / √2 ) + √72 = ( 8√2 / 2 ) + 6√2 = 10√2
問2
解答・解説
( ア ) ( x + 3 )2 – ( x + 2 ) ( x – 4 )
= x2 + 6x + 9 – ( x2 – 2x -8 ) = 8x + 17
( イ ) ( x + 1 )2 – 2 ( x + 1 ) -15 を因数分解します。
A = x + 1 とすると
A2 – 2A – 15 = ( A – 5 ) ( A + 3 ) となり、元に戻すと
( x + 1 – 5 ) ( x + 1 + 3) = ( x – 4 ) ( x + 4 )
( ウ ) 3x2 – 7x + 3 = 0 を解の公式を使って解きます。
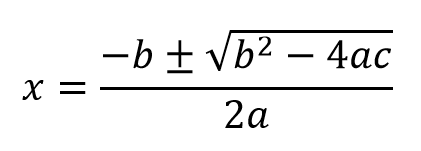
解の公式
x = ( 7 ± √13 ) / 6
( エ ) √2016n が自然数になる最も小さな n の値を求めます。
2016 を素因数分解します。
2016 = 2 × 2 × 2 × 2 × 2 × 3 × 3 × 7
このことから n = 2 × 7 = 14 であれば、√2016n の根号が外れることがわかります。
n = 14
2016年にちなんだ問題ですね
( オ ) ( – 1 / 2 ) x2 は、x = 0 のとき、y = 0 ( 最大値 ) を持つ上に凸の2次関数です。
x が 0 から離れるほど y は小さくなるので x = -6 のときに y は最小の値を持つことがわかります。
最小値 ｙ = ( – 1 / 2 ) × ( -6 ) × ( -6 ) = -18
よって、a = -18, b = 0 となります。
( カ ) 小さいほうの自然数を n とおきます。問題文より次の方程式が成立します。
n2 + ( n + 1 )2 = 113
式を展開し、因数分解すると
( n – 7 ) ( n + 8 ) = 0
n > 0 より
n = 7
( キ ) 中央値は数値を小さいほうから順に並べたときの真ん中の値です。資料の数が偶数個のときは、中央に位置する2つの値の平均をとります。
今回は資料の個数が偶数個なので中央に近い 94, 95 の平均となります。並び替えはやってみよう！
よって、中央値 = ( 94 + 95 ) / 2 = 94.5 となります。
( ク ) 下の図のように補助線を E から AB に向かって AD と平行となるようにひきます。
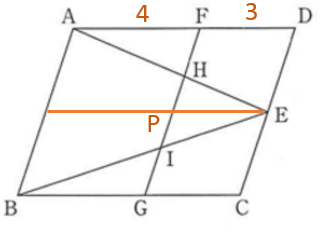
△BGI ∽ △EPI ( 相似比 4 : 3 ) なので、面積比は 16 : 9 となります。また、PE を底辺とする △EPI と △EPH の高さは等しいので面積も等しくなります。
これらから △BGI ：△EHI = 16 : ( 9 + 9 ) = 16 :18 = 8 : 9 がわかります。
問3
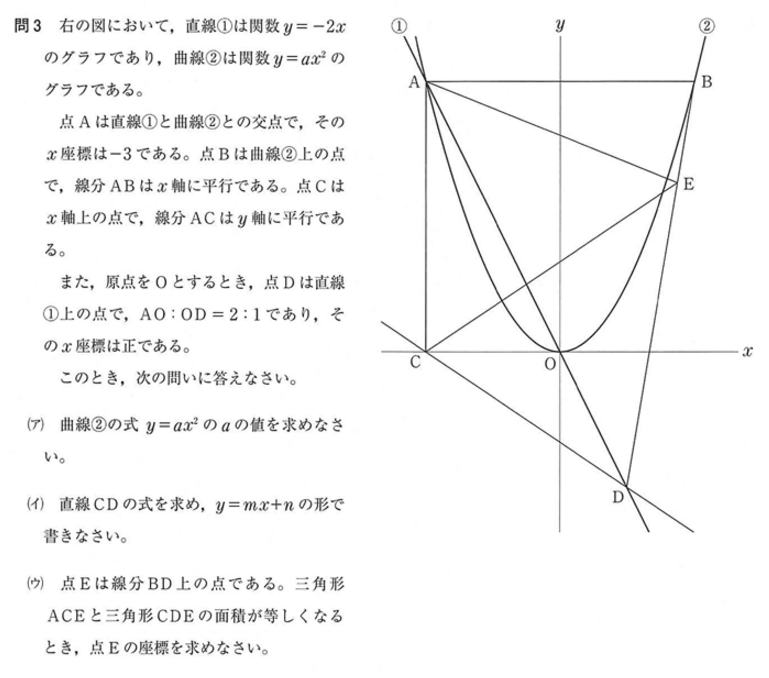
解答・解説
( ア ) 点A は直線①上にあり x = -3 なので、①に代入すると y = 6 であることがわかります。
点A ( -3, 6 )
点A は曲線②上の点でもあるので②に代入します。
6 = a × ( -3 ) × ( -3 )
よって、a = 2 / 3 となります。
( イ ) AO : OD = 2 : 1 なので、点D の x 座標は 3 /2 がわかります。そのときの y 座標は ①に代入して y = -2 × ( 3 / 2 ) = -3 であることがわかります。
点D ( 3 / 2 , -3 )
また、点C の座標は 点C ( -3, 0 ) であることから、2点C, D を通る直線の方程式を求めます。計算は省略します。レッツトライ！
y = ( – 2 / 3 ) x – 2
( ウ ) この問題はどのように解答すればよいかを最初にイメージできるかが鍵です。たくさんの問題をこなして試験に臨まないと解答するのは難しいかもしれません。
まずは直線BD の式を求めます。
点B ( 3, 6 )
点D ( 3 / 2, -3 )
より直線の式を求めると、
y = 6x – 12 となります。
点E の座標を E ( p, 6p – 12 ) とおくと
△ACE = ( 1 / 2 ) × 6 × ( 3 + p ) = 3 ( 3 + p ) = 3p + 9 となります。
△ECD は x 軸で 2つの3角形に分割してそれぞれ面積を求めます。
x 軸より上の3角形の面積 = ( 1 / 2 ) × 5 × ( 6p – 12 )となるので、
x 軸より下の3角形の面積 = ( 1 / 2 ) × 5 × 3
△CDE の面積 = ( 1 / 2 ) × 5 × ( 6p – 12 ) + ( 1 / 2 ) × 5 × 3 = ( 30p – 45 ) / 2 となります。
△ACE = △CDE となることから
3p + 9 = ( 30p – 45 ) / 2 となる p を求めます。p を求めると
p = 21 / 8 が導かれますので、このときの y 座標を求めると
点E ( 21 / 8 , 15 / 4 ) となります 。
問4
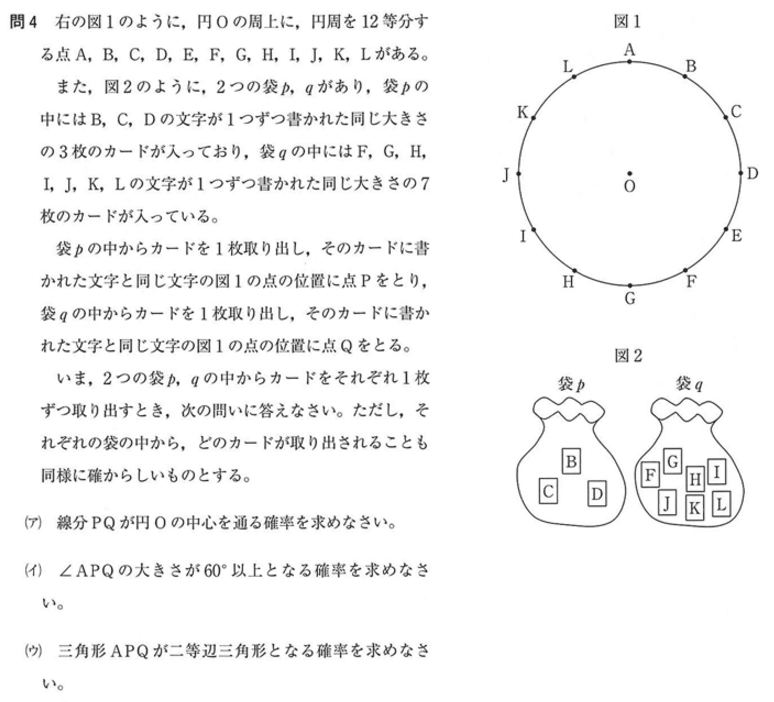
解答・解説
( ア ) カードを取り出すパターンは全部で 3 × 7 = 21 通りです。
次に円O の中心を通る取り出し方は次の3パターンです
( B, H ), ( C, I ), ( D, J )
よって求める確率は 3 / 21 = 1 / 7 となります。
( イ ) 下の図を確認しましょう。
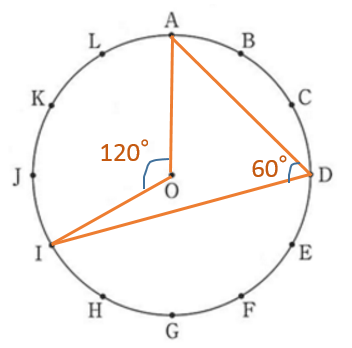
円周を12分割しているので、例えば取り出したカードが D, I のときに円周角の定理により、∠APQ は 60° となります。よって、D が 点P の時は Q が A から 4つ以上離れている場合に ∠APQ は 60° 以上の角度になることがわかります。これらのことを、B, C, D それぞれのときに当てはめて、60° 以上となる組み合わせをすべて抽出します。
レッツトライ！
洗い出すと全部で 12 パターンの組み合わせが見つかります。
よって求める確率は 12 / 21 = 4 / 7 となります。
( ウ )
この問題もパターンを1つずつ確認し二等辺三角形であるか確認して抽出するだけです。例えば △ADJ は二等辺三角形です。
すべてのパターンを確認すると5パターン二等辺三角形になることがわかります。
よって、求める確率は 5 / 21 です。
問5
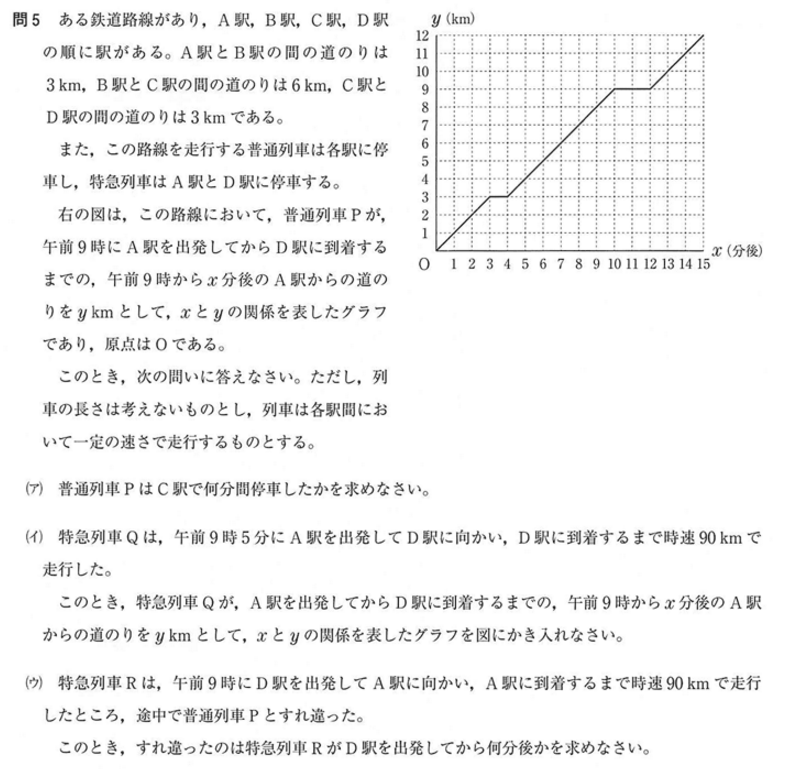
解答・解説
( ア ) グラフをみたまんまです。2分間停止しています。
( イ ) 時速90km であることから 1分間に 1.5km 進みます。これをグラフに書き込むと下のようになります。
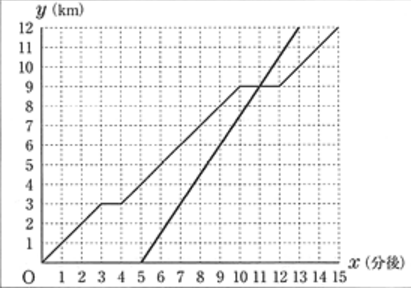
( ウ ) 特急列車R は9時に D 駅から A 駅に向かって時速90kmで進みます。グラフに書き込むと下の図のようになります。
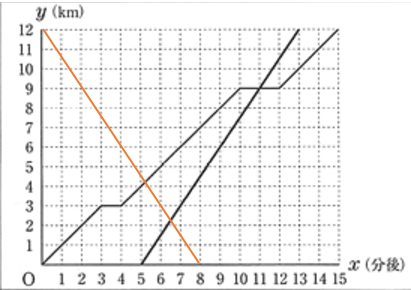8分間で特急列車RはA 駅に着きます。また、普通列車P とすれ違うのは P が B 駅と C 駅の間を走っているときであることがわかります。
2つの直線の交点を求めて、解答となります。
2直線の導出とその交点の計算はレッツトライ！
答えは、26 / 5 分後となります。
問6
解答・解説
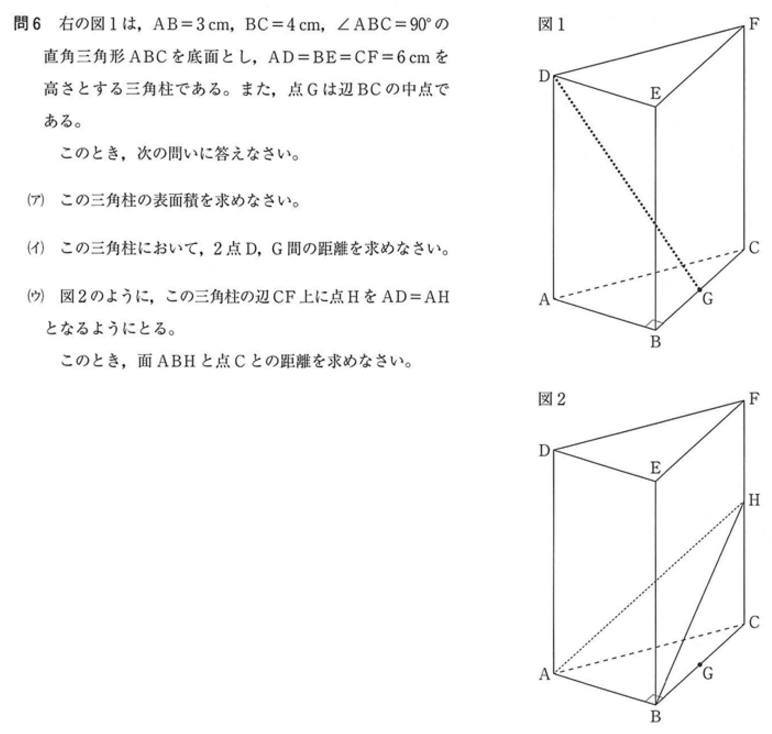
( ア ) まずはAC = 5 cm です。覚えておいてもよいでしょう。三平方の定理を使う場合は AC2 = 32 + 42 から AC を求めます。次に三角柱の展開図を考えます。三角形以外の部分は 6 × ( 3 + 4 + 5 ) の長方形になります。
よって、2つの三角形の面積と長方形の面積をすべて足して三角柱の面積を求めます。
三角柱の面積は 84 cm2 となります。
( イ )
AG2 = BG2 + AB2 = 22 + 32 から AG を計算します。
DG2 = AG2 + DA2 から DG を求めます。なお、DA = 6 cm です。
計算すると DG = 7 cm となります。
( ウ ) 直角三角形 △ACH に着目します。
三平方の定理より、AH2 = BC2 + CH2 ( AH = 6, AC = 5 ) より、CH を求めると
CH = √11 となります。
次に 直角三角形 △BCH において、三平方の定理より BH2 = BC2 + CH2 ( BC = 4, CH = √11 ) よりBH を求めると
BH = 3√3 となります。
△ABCを底面とする三角錐H-ABC の体積を求めると、
三角錐H-ABC の体積 = 2√11 cm3 となります。
次に、△ABH の面積は ( 1 / 2 ) × AB × BH より、( 9√3 / 2 ) cm2 です。
次に △ABH を底面とする三角錐 C-ABH に着目します。体積は既にもとまっていますので、高さを h とすると
( ( 9√3 / 2 ) × h ) / 3 = 2√11 が成り立ちます。
h を求めると
h = 4√33 / 9 cm となり、これが求める距離となります。
問7
解答・解説
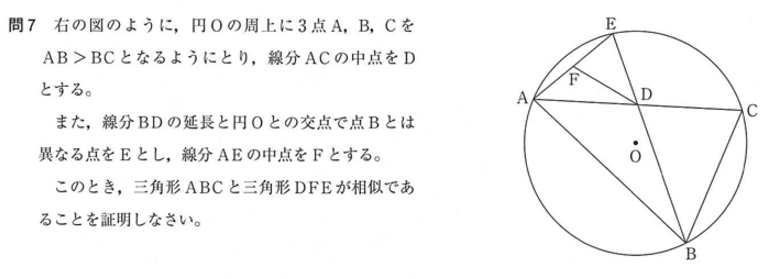
△ABC と △FDE において、弧AB の円周角は等しいので ∠ACB = ∠AEB であることから
∠ACB = ∠DEF ・・・①
次に、CE を結ぶ線をひきます。
弧BC の円周角は等しいので ∠BAC = ∠BEC
中点連結定理より CE // DF となり、平行線の錯角は等しいので ∠CED = ∠FDE となり、∠BEC = ∠FDE がわかります。
よって、∠BAC = ∠FDE ･･･②
①、②より、2組の角がそれぞれ等しいから、
△ABC ∽ △DEF
となります。