最大公約数や最小公倍数は小学生の算数で習います。ここでは一歩踏み込んで最小公倍数と最大公約数を図を使って確認していきます。すると、ちょっとビックリなことが発見できます。どのような発見でしょうか。
スポンサーリンク
例題
36 と 48 の最大公約数と最小公倍数を求めてみよう。
解答
ここでは、具体的な計算は行いません。答えだけ載せておきます。
最大公約数:12
最小公倍数:144
このページでは、ここからが本題です。
最小公倍数、最大公約数を図を使って理解する
まずは、例題の36, 48 を素因数分解してみます。小学生では習わない言葉ですが心配要りません。公約数や公倍数を計算で求めることができるのであれば、間違いなく理解できるものです。
36 = 2 × 2 × 3 × 3
48 = 2 × 2 × 2 × 2 × 3
まずは、上記の共通部分(赤字)とそうではない部分を分けて下図のように区分します。
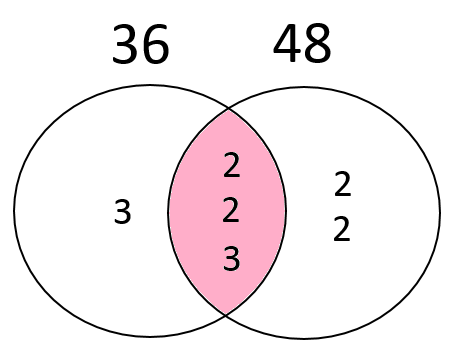
公約数と公倍数
36と48の共通部分とそうでない部分を図を使って分けてみました。ここからどのようなことがわかるのでしょうか。実は共通部分は最大公約数を表しています。そして、共通部分と残りの数字の積(掛け算の結果)が最小公倍数になります。
最小公倍数を求める場合、共通部分は1回だけ掛ければいいです。2回掛ける必要はありません。
最大公約数 = 2 × 2 × 3 = 12
最小公倍数 = 2 × 2 × 3 × 2 × 2 × 3 = 144
また、これらのことから難しい表現を使用すると、正の整数a, b に対して、それらの最大公約数を g、最小公倍数を l とおくと a × b = g × l であることがわかります。上記の例を使って具体的にいうと、36 × 48 = (36 と 48 の最大公約数) × (36 と 48 の最小公倍数) です。検証してみます。
a × b = 36 × 48 = 1728
(最大公約数) × (最小公倍数) = 12 × 144 = 1728
となり、計算結果がピタリと一致しました。どうでしょうか、驚きはありましたでしょうか。

おっ!