2直線を表す方程式について考えてみたいと思います。そもそも2直線を表す方程式とはどのようなものでしょうか。それは、以下のような方程式です。
スポンサーリンク
2直線を表す方程式 : (ax + by + c) (dx + ey + f) = 0
上記のように直線を表す方程式の積で、2直線を表すことができます。では、このことを利用するよくある例題を確認していきたいと思います。
問題
2x2 + kxy – 12y2 + x + 7y – 1 = 0 が2直線を表わすように定数 k の値を求めよ。
解答
2x2 + kxy – 12y2 + x + 7y – 1 = 0 が、2直線を表す方程式の形 (ax + by + c) (dx + ey + f) = 0 に因数分解できることができるように定数 k を求めていきます。
2x2 + kxy – 12y2 + x + 7y – 1 = 0
を x について整理します。
2x2 + (ky + 1)x + ( – 12y2 + 7y – 1) = 0 ・・・ ①
上記の式は、x について、ax2 + by + c = 0 の形に整理した式です。次に解の公式を見てみましょう。
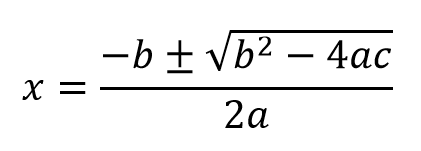
解の公式
①式の解が、x が y の1次式となるには、根号が1次式として外れることが必要十分条件となります。すなわち根号内の
D = b2 – 4ac
= (ky + 1)2 – 4×2( – 12y2 + 7y – 1)
= (k2 + 96)y2 + 2(k – 28)y + 9
が y の完全平方式でなければいけません。y の完全平方式であれば、= 0 としたときに重解(実数解が1つ)を持ちますので、
(k2 + 96)y2 + 2(k – 28)y + 9 = 0 ・・・ ②
が重解を持つように k を求めることになります。
ここで再度、解の公式の登場です。②式が重解を持つのであれば、根号内 b2 – 4ac = 0 ですので、
{2(k – 28)}2 – 4 × (k2 + 96) × 9 = 0
となり、展開および整理すると
k2 + 7k + 10 = 0
(k + 5) (k + 2) = 0
よって、k = -5, -2 が求まります。
ポイント
- 完全平方式 ⇔ = 0 としたとき重解をもつ
- 重解を持つということは、判定式 D = 0 ( b2 – 4ac = 0 )
例) y が重解を持つような2次方程式
(ay – b)2 = 0
y = b / a の重解を持ちます。
解の公式が大活躍しました。「申」が始まりました。良い1年になりますように。
https://hensa40.cutegirl.jp/archives/618
k x y+2 x^2+x-12 y^2+7 y-1 を
斉次化し k X Y+2 X^2+X Z-12 Y^2+7 Y Z-Z^2.
対応する M={{2,k/2,1/2},{k/2,-12,7/2},{1/2,7/2,-1}}を求め
その行列式=0 KARA k=-5,k=-2 を瞬時にゲットし Fin.
(<—- そんな ことする奴 おらん! と 云われそう…)
https://www.youtube.com/watch?v=zYoYoBtLqOY
(1+x-3 y) (-1+2 x+4 y) と (1+x-4 y) (-1+2 x+3 y) と正鵠を射る。
他の 多様な 特に ●特異点 を 求める 発想で●
解答を お願い致します;
————————————————————————
●singularity● に ついて
世界の聴衆________名 が 聴きいっています。
理解者が 殆ど全て なのでしょう……….
長時間に亘る が 細部をも 聴き取り 解説を 是非 お願い致します;
https://www.youtube.com/watch?v=H9s17WE6CL4