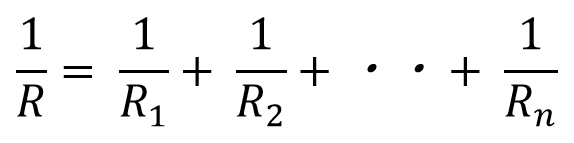例えば、a と b の平均を (a + b) / 2 のように計算する方法は相加平均と言われています。ここでは、調和平均と呼ばれている平均を計算してみたいと思います。
スポンサーリンク
調和平均の計算方法
調和平均は、以下のように計算します。調和平均をHとすると、
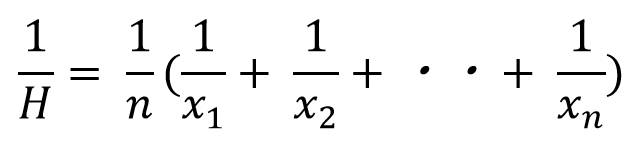
調和平均Hの計算方法
実は以下のリンクで平均速度を求めているのですが、それが調和平均の考え方です。時間があれば参照ください。ここでは、気楽に読める別の例を紹介します。
例えば、A君とB君が500円ずつお小遣いを持って、お菓子を買いに言ったとします。A君は100円のお菓子を5個、B君は20円のガムを25個買ったとします。A君とB君が購入したすべての商品1個あたりの平均金額はいくらでしょうか?
ここで、(100 + 20) / 2 = 60円 と計算すると管理人と同じレベルです。A君の購入単価は 100円です。B君の購入単価は 20円です。ここまではよいのですが、ここから先がNGです。
お店の人の立場になって考えて見ましょう。お店の人からすると、2人の合計購入金額は 500 + 500 = 1,000円です。商品の販売個数はA君が5個、B君が25個なので、合計30個になりますね。従って1商品あたりの購入単価は、( 1000 / 30 ) ≒ 33.3 円となります。
では、式に当てまめてみます。
1 / H = ( (1 / 100) + (1 / 20) ) / 2 = (6 / 200)
H = 200 / 6 ≒ 33.3 となりますね。調和平均恐るべしです。
合成抵抗と調和平均
中学生の方であれば、理科で合成抵抗を求める公式をご存知の方も多くいらっしゃると思います。以下のような公式ですね。
調和平均とそっくりではないでしょうか。まずは、抵抗の数が2個の場合の合成抵抗を考えてみたいと思います。抵抗数2個の場合は、1 / R = (1 / R1) + (1 / R2) なとなり、R について解くと、R = R1R2 / (R1 + R2) になります。抵抗1個あたりの平均値は、合成抵抗の2倍となりますので、2R となります。
2個の並列接続の合成抵抗は和分の積 ab / (a+b) のように覚えているかも知れませんが、この公式でn=2 の時の展開式がそのようになるということです。
感の鋭い方なら気づきましたでしょうか。ここに調和平均が隠れています。合成抵抗R × 抵抗数 = 抵抗1個あたりの平均がわかります。合成抵抗の逆数(1/ R) を、抵抗1個あたり平均値 (n / R) に置き換えると調和平均の計算式そのものが出現します。
つまり、単純に回路数の調和平均を求めると、回路全体でみたときの、抵抗1個あたりの平均値を求めることができ、さらに抵抗数で割ることで、回路全体の合成抵抗を求めることができることを意味しています。上図の並列接続の合成抵抗Rを求める公式は、合成抵抗を求めるために、始めから抵抗数nで割ってあるために、微妙に調和平均の計算式と相違がでていたんですね。
お菓子から速度から合成抵抗まで色んなところに調和平均が出現しますね