扇形の面積を半径・中心角・弧の長さから求める2通りの方法

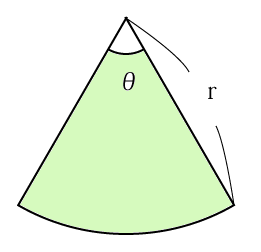
ここでは、扇形の面積を2通りの方法で求める例を図を示して掲載しています。扇形は凄いですよ。形からも想像できるように円と密接に関連しています。

半径と中心角から扇形の面積を求める

扇形の面積の求め方は、半径と中心角から求める方法が一般的です。

扇形の面積は、半径　×　半径　×　円周率　×　θ　/　360　で求めることができます。半径rの円の面積の θ / 360 倍の大きさで求める方法です。頭の中に大きな円はイメージできていますか？

弧の長さと半径から扇形の面積を求める

実は扇形の場合は、中心角がわからなくとも半径と弧の長さがわかればその面積を求めることができます。

扇形の面積　＝　弧の長さ　×　半径　÷　2

なんとなく、三角形の面積と同じように面積を求めることができてしまうのです。では、どうしてこのようなことがいえるかを考えて見ましょう。

扇形の面積を求める公式は前に述べたとおり以下の公式です。

扇形の面積　＝　半径　×　半径　×　円周率　×　θ　/　360　・・・　①

次に弧の長さを求めると以下のようになります。

弧の長さ　＝　円周　×　θ　/　360

＝　２　×　半径　×　円周率　×　θ　/　360

この式を変形すると、

弧の長さ　÷　２　＝　半径　×　円周率　×　θ　/　360　・・・　②

となります。

①と②の赤字部分を見てください。同じですよね。ここで②の左辺を①に代入すると、以下の式が出現します。

扇形の面積　＝　半径　×　弧の長さ　÷　２

扇形って凄いのね