ここでは、平成27年 ( 2015年 ) の東京都の高校入試数学の解説をしています。
スポンサーリンク
問1

解答・解説
[問1] -7 + 8 ÷ ( 1 / 2 )
= -7 + 8 × 2 = -7 + 16 = 9
[問2] 9a + 4b – ( a – 3b )
= 9a + 4b – a + 3b
= 9a – a + 4b + 3b
= 8a + 7b
[問3] ( √6 + 5 ) ( √6 – 2 )
= 6 + ( 5 – 2 ) √6 + 5 × ( -2 )
= 6 + 3√6 – 10
= 3√6 – 4
[問4]
x – 7 = 9 ( x + 1 )
x – 7 = 9x + 9
9x – x = -7 – 9
8x = -16
x = -2
[問5]
x – 2y = 6 より、x = 2y + 6 ・・・①
①式を、3x + 4y = 8 に代入します。
3( 2y + 6 ) + 4y = 8
6y + 18 + 4y = 8
10y = -10
y = -1
y = -1 を①式に代入します
x = 2 × ( -1 ) + 6 = 4
( x, y ) = ( 4, -1 )
[問6] x2 + 5x – 3 = 0
解の公式を使って求めます。
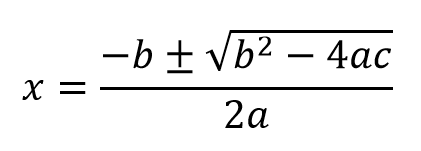
解の公式
x = ( -5 ± √37 ) / 2
[問7]
y = ( 1 / 3 ) x2
x = 6 のとき、y = 12
x = 9 のとき、y = 27
変化の割合 = ( y の増加量 ) / ( x の増加量 )
( 27 – 12 ) / ( 9 – 6 ) = 15 / 3 = 5
[問8]
( 少なくとも1個は白玉の確率 ) = 1 - ( 2個とも赤玉の確率 )
赤①、赤②、赤③、白①、白②とします。
5個の玉から2個取り出すパターンは、
( 5 × 4 ) ÷ 2 = 10通り
[ 白①, 白② ] と [ 白②, 白① ] は同じものだから2で割っています。
このうち2個とも赤色の場合は、
[ 赤①, 赤② ] [ 赤①, 赤③ ] [ 赤②, 赤③ ] の3通り。
したがって、
1 – ( 3 / 10 ) = 7 / 10
[問9]
A から BC の中点に向かって線をひきます。点B, C から等距離の円の交点を結んだ線と BC の交点が BC の中点になります。

問2

解答・解説
四角形ABQP は台形であり、AP = CQ = b cm, PD = BQ = c cm なので、
台形の面積の公式 ( 上底 + 下底 ) × 高さ ÷ 2 より、
S = ( 1 / 2 ) × a × ( b + c ) cm2
答えは b + c

解答・解説
n 段目の紙の枚数は、( n – 1 ) 枚であることがわかります。
また、この図形の面積 T は、すべての段が 1 段目と n 段目の合計値 2 + ( n + 1) = ( n + 3 ) となるように紙を並べてできる長方形の面積の半分であることから、
T = n × ( n + 3 ) × (1 / 2 )
であることがわかります。
問3

解答・解説
[問1]
点P は 直線 y = x – 4 上の点なので、 y = -2 のときは、-2 = x – 4 から、
x = 2
[問2]
直線 m は、点A ( 0, 6 ), 点B ( 4, 0 ) を通る直線となりますので、
傾き : -( 3 / 2 ), 切片 6 となることから
直線 m : y = -( 3 / 2 ) x + 6
[問3]
PQ = a とおくと、△BPQ は QB = QP の直角二等辺3角形なので、その面積は
( a2 / 2 ) cm2 ・・・①
となります。
△ACP において、AC = 10 cm を底面とすると、その高さは、OB + BP = ( a + 4 ) cm なので面積は
( 10 × ( a + 4 ) ) / 2 cm2 ・・・②
となります。
①、②の面積比が 1 : 5 なので、
5 × ( a2 / 2 ) = ( 10 × ( a + 4 ) ) / 2
この式を解くと
( a – 4 ) ( a + 2 ) = 0
a > 0 より、
a = PQ = 4 cm となります。
問4

解答・解説
[問1]
AB = AC より、∠ABC = ∠ACB = 75° であるから、△ABC の ∠CAB = 180 – ( 75 + 75 ) = 30° です。
△ABP に着目すると、∠ABP + ∠BAQ = ∠BQC であることから
∠BQC = a + 30 で表され、∠PQC = 180 – ∠BQC より、
∠PQC = ( 150 - a )°
[問2]
仮定より
AB = AC ( 二等辺三角形 )・・・①
BP = CR ・・・②
弧AP の円周角は等しいので
∠ABP = ∠ACR ・・・③
①、②、③より
二辺とその間の角がそれぞれ等しいから、
△ABP ≡ △ACR
[問3]
AB = BP = 9 cm であることから、△BPA は二等辺三角形であることがわかります。また、弧AB の円周角は等しいので、∠ACB = ∠APB です。これらのことから、△ABC ≡ △BPA となります。よって、△ABC ≡ △BPA ≡ △ACR であることがわかりました。
このことから、△APR は AP = AR の二等辺三角形であり、△ABC ∽ △APR であることがわかります。
相似であることから AB : BC = AP : PR = 9 : 6 = 3 : 2 となります。 AP = 6 であることこから PR = 4 cm がわかります。CP = 9 cm であることから
CP = 9 – 4 = 5 cm
問5

解答・解説
[問1]
BD = CD = PD = 4 cm となるので、△BCP は3辺が等しくなるので正三角形となる。
よって、
∠BPC = 60°
[問2]
BD = CD = 4 cm で、∠CDB は90° なので、三平方の定理より、また、BC = 4√2 です。M は BC の中点であることから BM = CM = 2√2 です。同様に三平方の定理より、DM = 2√2 であることもわかります。
次に、△AQP と △ADM に着目します。
∠AQP = ∠ADM = 90°
∠QAP = DAM ( 共通 )
より、△AQP ∽ △ADM です。
また、△ADM は直角三角形なので、三平方の定理より AM = 6√2 です。
△AQP ∽ △ADM より、
- AM : DM = AP : PQ より、6√2 : 2√2 = 6 : PQ から PQ = 2
- AM : AD = AP : AQ より、6√2 : 8 = 6 : AQ から AQ = 4√2
よって、MQ = AM – QA = 6√2 – 4√2 = 2√2 となります。
以上から、立体P-QBC ( 三角錐 ) の体積は
( ( (BC × QM ) / 2 ) × QP ) / 3 を計算して
( 16 / 3 ) cm3
となります。