ここでは、平成27年埼玉県高校入試数学の解説を行っています。
スポンサーリンク
問1

解答・解説
(1) 8x – 4x = 4x
(2) 5 + 3 × ( -2 ) = 5 – 6 = -1
(3) √24 – √6 = 2√6 – √6 = √6
(4) x2 + 8x + 16 = ( x + 4 )2
x = -4 + √2 を代入すると、
( -4 + √2 + 4 )2 = ( √2 )2 = 2
(5) 5x2 -3x -1 = 0
解の公式を使います。
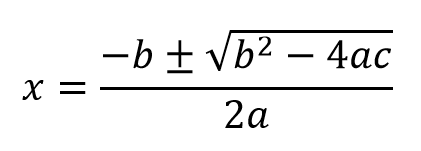
解の公式
解の公式より
x = ( 3 ± √29 ) / 10
(6)
x + 3y = 4 ・・・①
2x + 5y = 6 ・・・②
①より
x = 4 – 3y を②式に代入します。
2( 4 – 3y ) + 5y = 6
8 – 6y + 5y = 6
y = 2
①式に y = 2 を代入します。
x + 3 × 2 = 4
x = -2
(7) -2 ≦ x ≦ 3 のとき
x = 0 のとき、y が最大値 0 となります
x = 3 のとき、y が最小値 -9 となります
-9 ≦ y ≦ 0
(8) 取り出した黒玉の割合は 35 / 56
480 × ( 35 / 56 ) = 300
300 個

解答・解説
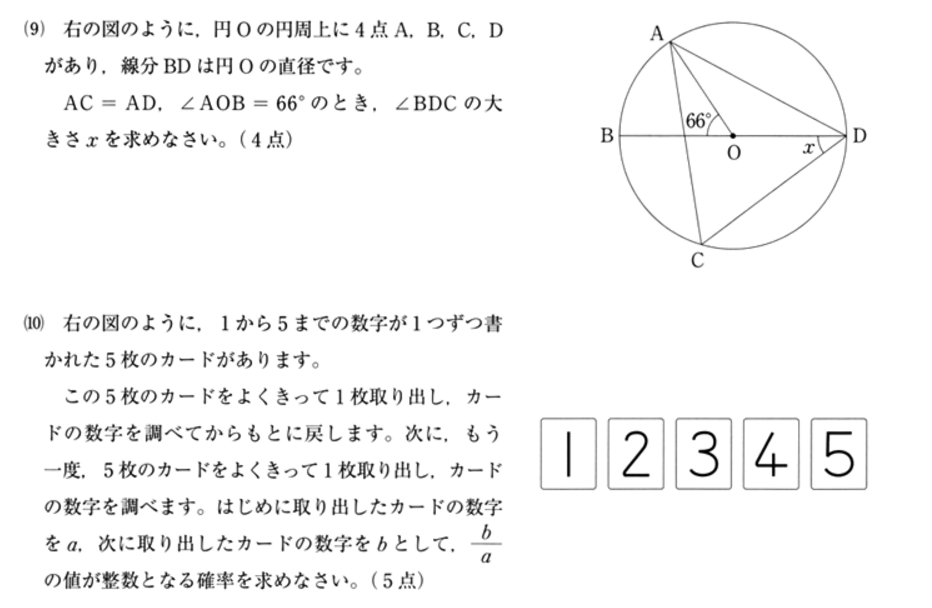
(9) ∠BDC を求めます。
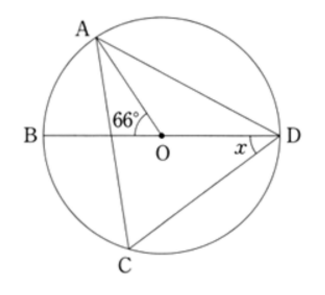
∠AOD = 180 – 66 = 114°
∠ACD = 114 / 2 = 57°
∠ADO = 66 / 2 = 33°
AC = AD より、
x + ∠ADO = ∠ACD
x + 33 = 57
x = 24
(10) カードを取り出すパターンは全部で 5 × 5 = 25 通り
b / a が整数になるパターンは
( a, b ) = ( 1, 1 ) , (1 , 2), ( 1, 3 ), ( 1, 4 ), ( 1, 5 )
( a, b ) = ( 2, 2 ) , (2 , 4)
( a, b ) = ( 3, 3 )
( a, b ) = ( 4, 4 )
( a, b ) = ( 5, 5 )
の10パターンなので、求める確率は
10 / 25 = 2 / 5
(11) ① 4回
2000年:4で割り切れ、100でも割り切れるが、400でも割り切れるのでうるう年
2004年:4で割り切れるのでうるう年
2008年:4で割り切れるのでうるう年
2012年:4で割り切れるのでうるう年
(11) ② うるう年ではない年 365 ÷ 7 = 52 余り 1 なので、翌年の誕生日は曜日が1つずれる
例)月曜日 ⇒ 火曜日
うるう年では 366 ÷ 7 = 52 余り 2 なので、翌年の誕生日は曜日が2つずれる
例)月曜日 ⇒ 水曜日
2015年 : 月曜日
2016年 : 水曜日 (うるう年)
2017年 : 木曜日
2018年 : 金曜日
2019年 : 土曜日
2020年 : 月曜日 (うるう年)
よって、2020年
2020年は東京オリンピックです。オリンピックにちなんで出題されたものと思われます。
問2
解答・解説
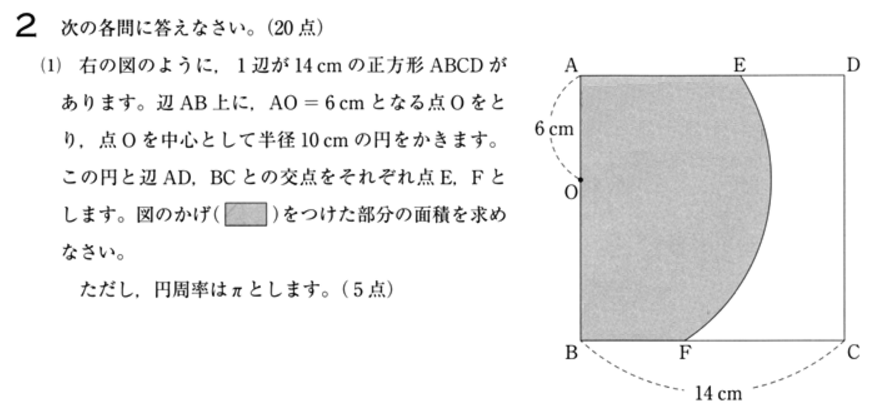
(1) 問題文からわかっていることを整理すると下の図のようになります。
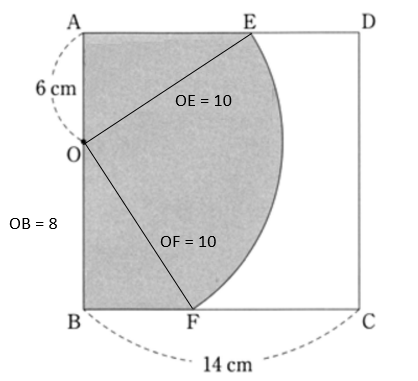
また、△AOE と △OBF は直角三角形なので、三平方の定理より
AE = 8 と、BF = 6 が求まります。
直角三角形の辺の比 3:4:5 を覚えておくと計算の手間が省けます。覚えておきましょう。
また、△AOE と △OBF が合同であることから、∠EOF = 90° であることもわかります。
求める面積 = △AOE の面積 + △OBF の面積 + 中心角90°の扇形の面積
を計算すると
25π + 48 cm2
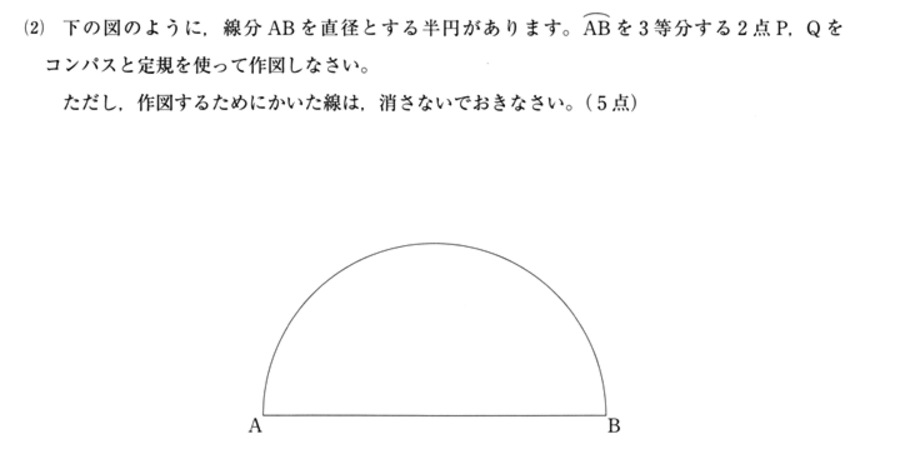
解答・解説
ここでは、解答例のみの掲載となります。
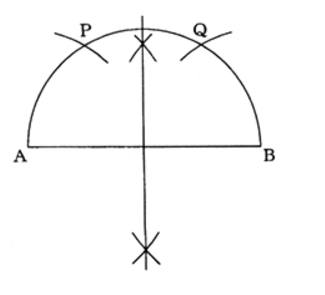
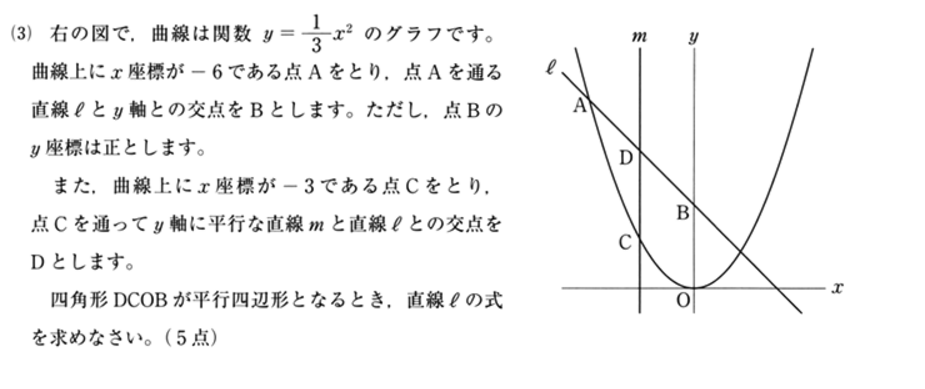
解答・解説
四角形DCOB が平行四辺形になるためには、DB // CO である必要があります。
点C ( x, y ) = ( -3, 32 / 3 ) = ( -3, 3 ) より、CO の傾きは -1 なので、直線 ℓ の傾きも -1 であることから
直線 ℓ : y = -x + b と表せます。また、ℓ は点A ( x, y ) = ( -6, 12 ) を通るので
12 = 6 + b より、b = 6 となります。
よって、直線 ℓ は y = -x + 6
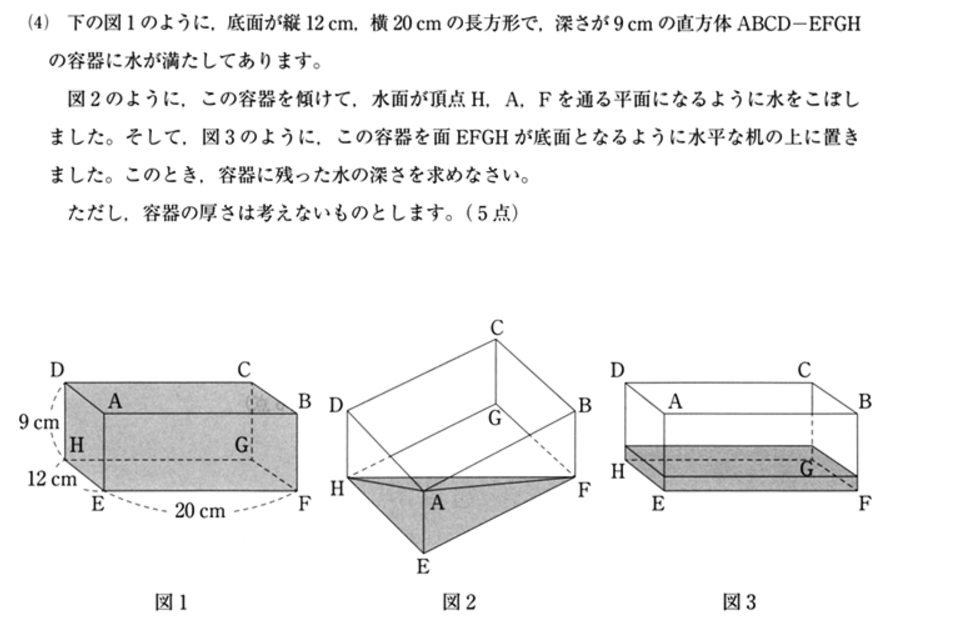
解答・解説
図2 において、△AHE を底面とする三角錐を考えます。
△AHE の面積 : 12 × 9 × ( 1 / 2 )
三角錐の高さは EF = 20
より、
三角錐の体積 = 12 × 9 × ( 1 / 2 ) × 20 × ( 1 / 3 ) ・・・①
図3の水面までの高さを x とすると
体積は、
12 × 20 × x ・・・②
で求めることができます。
①と②は等しいので方程式を解くと
x = ( 3 / 2 ) cm3
が求まります。
∠HEF が直角であることがポイントです。
問3
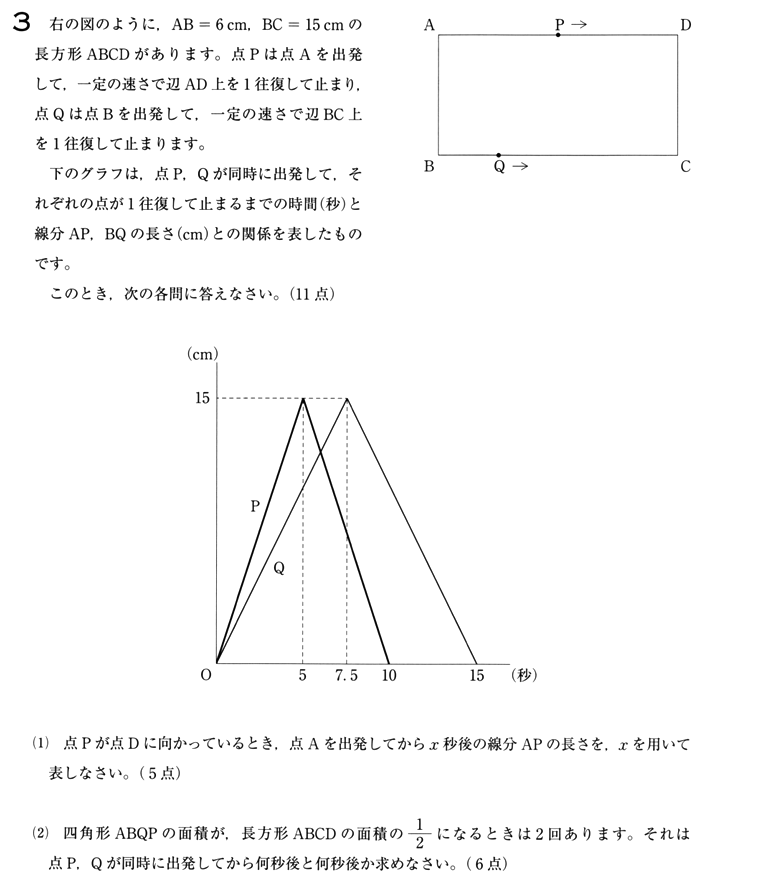
解答・解説
(1)
点Pは5秒後に D に到着しているので、1秒間当たり 3 cm 進むことがわかります。
よって、AP の長さは 3x cm です。
(2)
BP の長さは 7.5秒後に C に到着しているので 1秒当たり 2 cm 進みます。
よって、BP の長さは 2x cm です。
x 秒後の四角形ABQPの面積を場合分けして考えます。
- 0 ≦ x < 5 の場合
P, Q が共に D, C に向かっている場合です。
四角形ABQPの面積を S とすると、
S = ( AB × AP ) / 2 + ( AB × BQ ) / 2
= ( 6 × 3x ) / 2 + ( 6 × 2x ) / 2
= 9x + 6x
= 15x
四角形ABCD の面積は 6 × 15 = 90 cm2 なので
S = ( 90 / 2 ) = 45 cm2 となる x を求めます。
15x = 45 から
x = 3 が求まります。また、0 ≦ x ≦ 5 とも矛盾しません。
- 5 ≦ x < 7.5 の場合
P は 折り返しているが、Q は C に向かっている時間帯です。
AP の長さは ( 30 – 3x ) cm で表されます。
直線の方程式 ( AP の長さ ) は 5秒後以降の傾きと切片から求めます。
四角形ABQPの面積を S とすると、
S = ( AB × AP ) / 2 + ( AB × BQ ) / 2
= ( 6 × ( 30 – 3x ) ) / 2 + ( 6 × 2x ) / 2
= 90 – 9x + 6x
= -3x + 90
-3x + 90 = 45 となる x を求めると
x = 15 となり、5 ≦ x < 7.5 の範囲にないので求める結果ではありません。
- 7.5 ≦ x < 10 の場合
P, Q 共に折り返している状態です。また、10秒後には P が A に着いてしまうので、10秒後には四角形ABQP が作れなくなります。
AP の長さは ( 30 – 3x ) cm で表されます。
BQ の長さは ( 30 – 2x ) cm で表されます。
四角形ABQPの面積を S とすると、
S = ( AB × AP ) / 2 + ( AB × BQ ) / 2
= ( 6 × ( 30 – 3x ) ) / 2 + ( 6 × ( 30 – 2x ) ) / 2
= 90 – 9x + 90 – 6x
= -15x + 180
-15x + 180 = 45 となる x を求めると
15x = 180 – 45 = 135
x = 9 となり、7.5 ≦ x < 10 とも矛盾しません。
問4

解答・解説
(1)
∠BAC = ∠FAC であることは明らかです。折ってますから。
また、AB // CD の錯角であるため、
∠BAC = ∠FCA
よって、∠FAC = ∠FCA であることから
△ACF は 二等辺三角形です。
(2)
下の図を見て下さい。
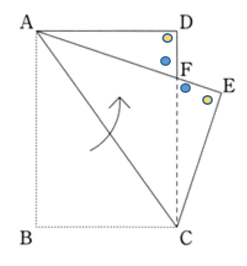
△AFD と △CFE において
∠CFE = ∠AFD (対頂角)
∠ADF = ∠CEF = 90°
また、AF =CF であるので、
△AFD ≡ △CFE がわかります。
FE = x とおくと、
FE = x、CF = 12√2 – x , CE = 12 から
直角三角形 CEF において、三平方の定理より、
FE2 + CE2 = CF2
に代入して値を求めて、x を求めると
x = FE = 3√2 cm が求まります。
△AFD ≡ △CFE の部分は不要でした。折角なので残しておきます。
(3)
△AIJ = △AHJ - △AHI の方針で求めていきます。
△AHJ ≡ DFJ なので、△AHJ の AH を底辺としたときの高さは
AD / 12 = 6 となります。
AH は (2) で求めた FE と等しいので 3√2 cm です。
これで、△AHJ の面積の計算ができます。レッツトライ!
次に △AHI ∽ △CDI であり、相似比は AH : CD から
1 : 4 であることがわかります。
△AHI において、底辺を AH としたときの高さは、相似比より
12 × ( 1 / 5 ) であることがわかります。
これで、△AHI の面積も求めることができます。
△AIJ の面積 = △AHJ の面積 - △AHI の面積
( 27√2 ) / 5 cm2 となります。