ここでは、平成26年北海道高校入試数学の過去問解説を行っています。
スポンサーリンク

解答・解説
(1) 5 – 7 = -2
(2) -6 + 9 ÷ 1 / 4 = -6 + 9 × 4 = -6 + 36 = 30
(3) 3√2 × √8 = 3√2 × 2√2 = 3 × 2 × √2 × √2 = 6 × 2 = 12
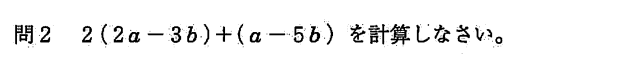
解答・解説
2 ( 2a – 3b ) + ( a – 5b ) = 4a – 6b + a – 5b = 5a – 11b
解答・解説
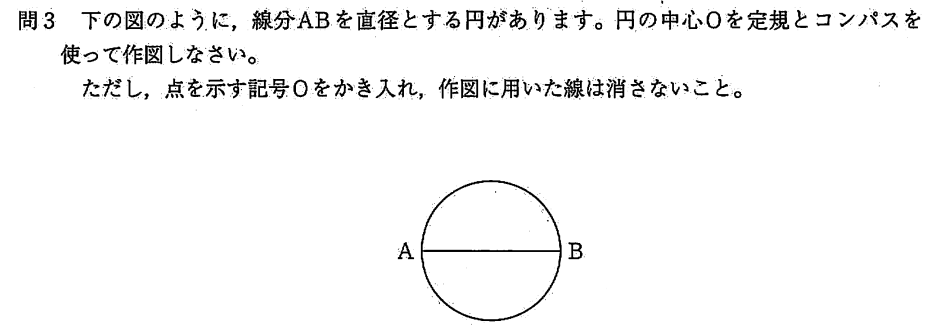
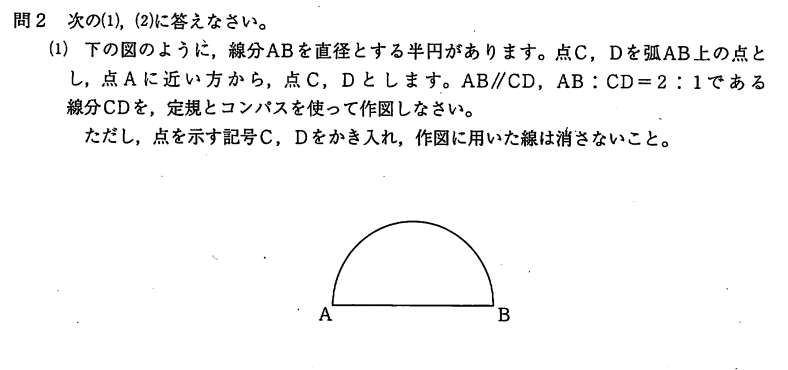
点A, B から等距離となるようにコンパスで交点を作図して結びます。
解答・解説
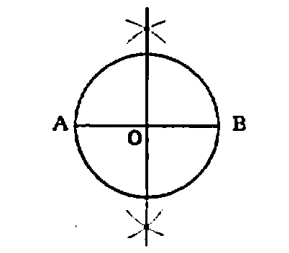
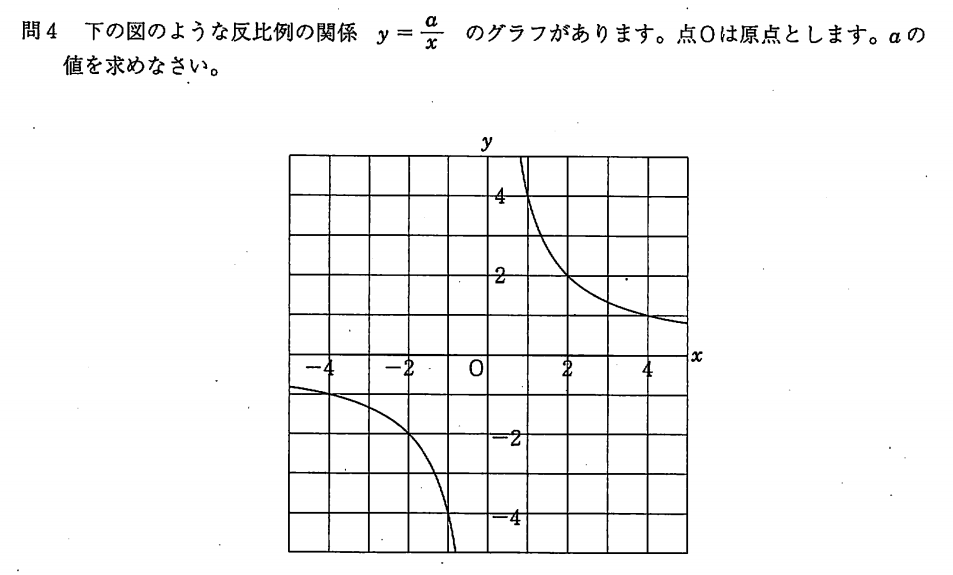
y = a / x は上の図より、( x, y ) = ( 2, 2 ) を通るので反比例の式に代入します。
2 = a / 2 より
a = 4
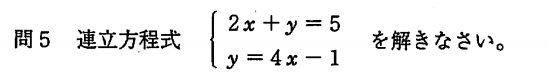
解答・解説
y = 4x – 1 を 2x + y = 5 に代入します。
2x + 4x – 1 = 5
6x = 6
x = 1
y = 4x – 1 に x = 1 を代入します。
y = 4 × 1 – 1 = 4 – 1 = 3
よって、( x, y ) = ( 1, 3 )
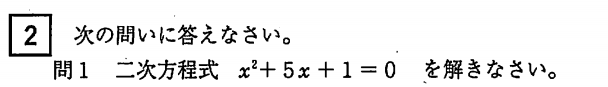
解の公式を使います。
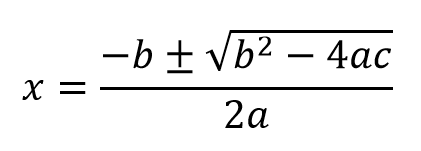
解の公式
解の公式より、
x = ( -5 ± √21 ) / 2
解答・解説
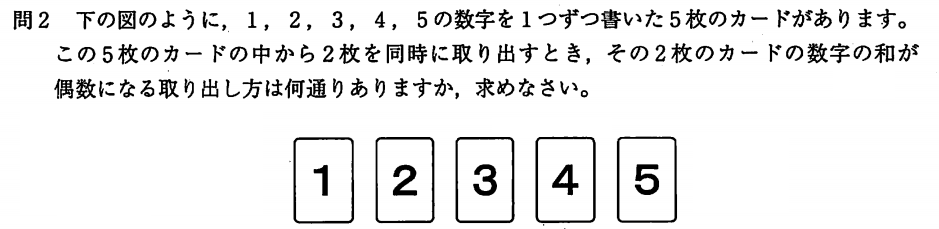
2枚のカードの数字のわが偶数になるのは、2枚とも奇数、または2枚とも偶数のときになります。組み合わせは下記の通りとなります。
( 1, 3 ), ( 1, 5 ), ( 3, 5 ), ( 2, 4 ) の4通り
解答・解説
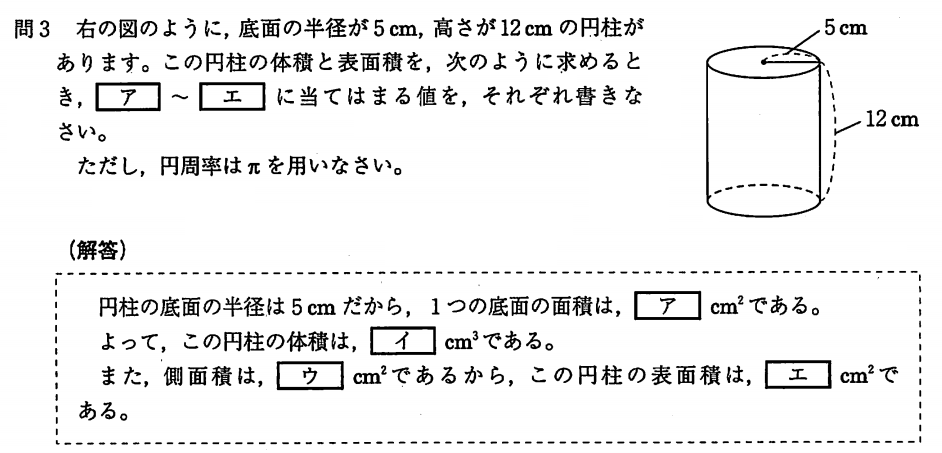
( ア ) 5 × 5 × π = 25π
( イ ) 底面積 × 高さ = 25π × 12 = 300π
( ウ ) 底面の円周 × 高さ = 10π × 12 = 120π
( エ ) 側面積 + 底面 × 2 = 120π + 25π × 2 = 170π

解答・解説
( x + 10 ) / 3 = ( x – 6 ) / 2
両辺を 6倍します。
2( x + 10 ) = 3( x – 6 )
2x + 20 = 3x – 18
x = 38
解答・解説
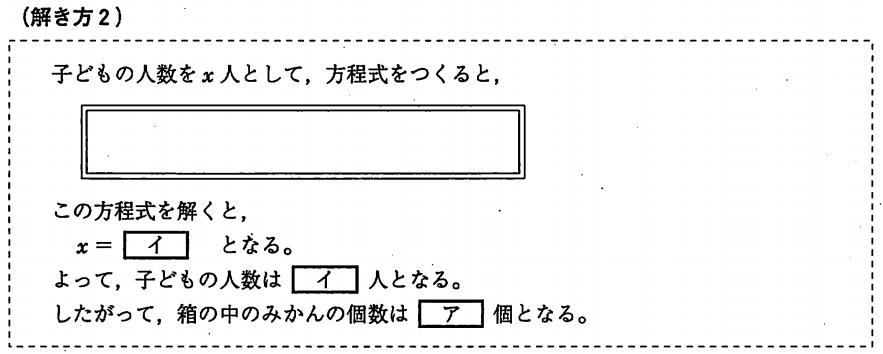
子供の人数を x とすると、
全員に3個ずつ配ると 10個足りず、2個ずつ配ると6個あまることから、
3x – 10 = 2x + 6
が成立します。
よって、子供の人数 x について解くと
x = 16 となります。

解答・解説
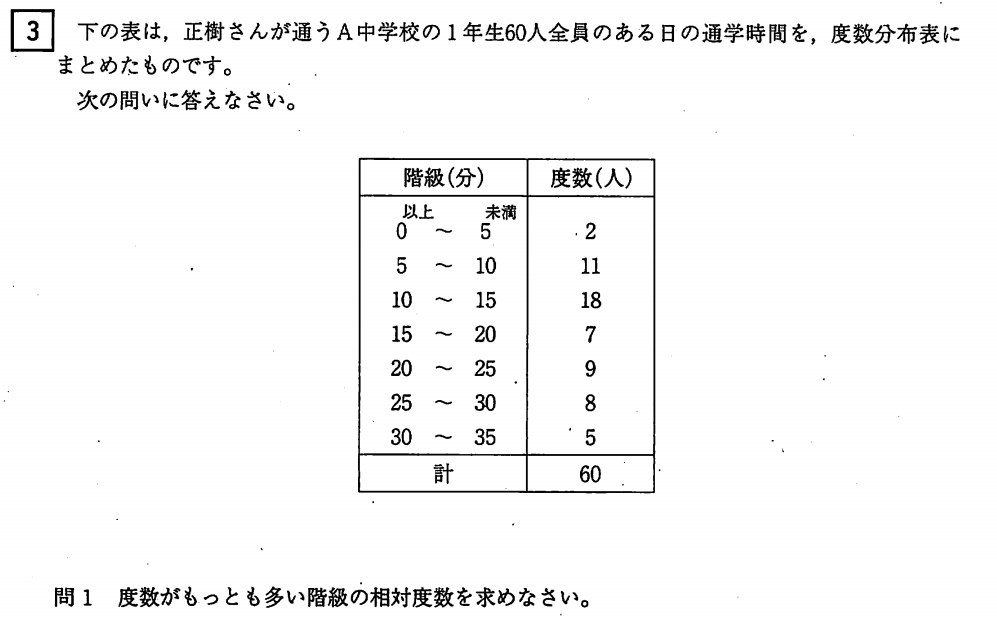
累積度数と相対度数を下表にまとめます。
- 度数分布表
| 階級 | 度数 | 累積度数 | 相対度数 |
|---|---|---|---|
| 0 以上 ~ 5 未満 | 2 | 2 | 2 / 60 = 0.0333 |
| 5 以上 ~ 10 未満 | 11 | 13 | 11 / 60 = 0.1833 |
| 10 以上 ~ 15 未満 | 18 | 31 | 18 / 60 = 0.3 |
| 15 以上 ~ 20 未満 | 7 | 38 | 7 / 60 = 0.1166 |
| 20 以上 ~ 25 未満 | 9 | 47 | 9 / 60 = 0.15 |
| 25 以上 ~ 30 未満 | 8 | 55 | 8 / 60 = 0.1333 |
| 30 以上 ~ 35 未満 | 5 | 60 | 5 / 60 = 0.0833 |
| 計 | 60 | – | – |
問1 は、最も度数の大きな階級の相対度数なので、上の表より 度数18 の階級の相対度数なので 0.3 となります。
問2 の解答例
通学時間が15分未満の生徒が 31 人いるから。
解答・解説
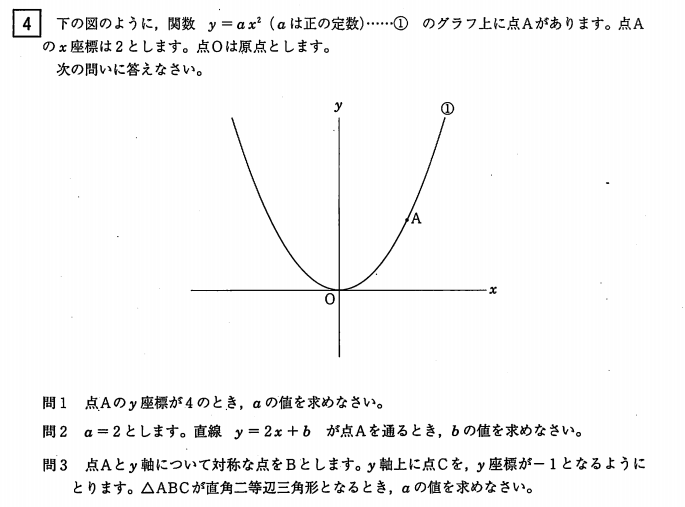
問1
( x, y ) = ( 2, 4 ) なので、y = ax2 に代入すると、
4 = a × 2 × 2
よって、a = 1
問2
a = 2 , x = 2 を y = ax2 に代入すると、
y = 2 × 2 × 2 = 8 がわかります。
( x, y ) = ( 2, 8 ) を通る直線 y = 2x + b は
8 = 2 × 2 + b より
b = 4
また、直線の式は y = 2x + 4 となります。
問3
問題文より、点B, C をグラフに書き込みます。
公開されている解答例とは異なる解法を使用しています。
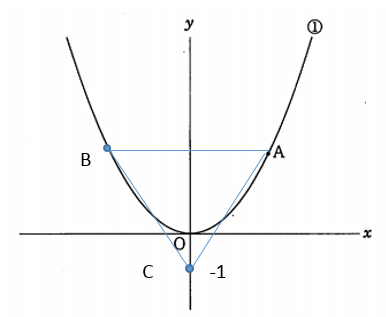
点A と点B は y 軸に対して対称なので AC = BC は明らかです。また、直角となりうるのは∠ ACB のみです。
∠ACB = 90° なので、三平方の定理より
AB2 = AC2 + BC2 ・・・①
また、
点A ( 2, 4a ) 点B ( -2, 4a ) 点C ( 0, -1 )
より、
AB2 = ( -2 – 2 )2 = 16
AC2 = BC2 = ( -2 – 0 )2 + ( 4a + 1 )2 = ( 4a + 1 )2 + 4
A = ( 4a + 1 )2 とおいて、式①に代入します。
16 = A + 4 + A + 4
2A = 8
A = 4 が求まりますので、
A = ( 4a + 1 )2 = 4
また、a > 0 より、
4a + 1 = 2
4a = 1
a = 1 / 4
解答・解説
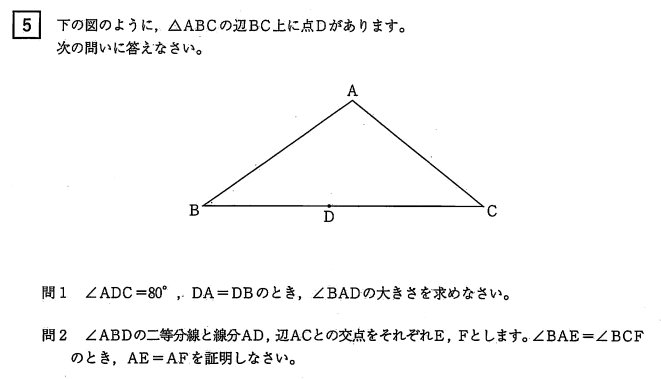
問1
∠ADC = 80° から ∠ADB = 100° となります。また、△ABD は DA = DB の二等辺三角形であることから、∠DAB = ∠DBA であることから、下の図のように角度が求まります。
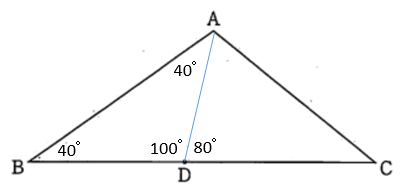
よって、∠BAD = 40° となります。
問2
問題文の通り、下の図に書き込むことからスタートです。
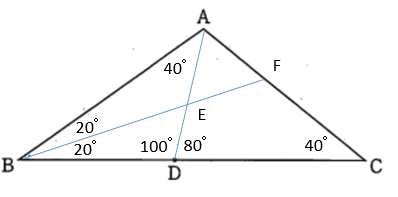
△ADC において、内角の和 = 180°より、∠DAC = 180 – ( 80 + 40 ) = 60°
△BDE において、内角の和 = 180°より、∠BED = 180 – ( 100 + 20 ) = 60°
また、対頂角より ∠BED = ∠AEF = 60°
三角形 ABF において、内角の和 = 180° より、∠AFE = 180 – ( 20 + 40 + 60 ) = 60°
以上から、△AFE は正三角形であることがわかります。
よって、AE = AF ( = EF )
学校裁量問題

解答・解説
問1 (1)
大した数でもありませんので、適当にアタリをつけて解答をだすこともできそうです。悩んだ場合には力技で回答してもよいでしょう。
(ア)、(イ)をそれぞれ、a, b とおくと、
ax + by = 10 ・・・①
ax – by = 2 ・・・②
①+②
2ax = 12
ax = 12
x = 12 / a
a は 1, 3, 5 であり、12 / a は整数であるので、
a = 1, x = 12 ・・・③
a = 3, x = 4 ・・・④
となります。
次に、①-②
2by = 8
by = 4
y = 4 / b
b = 2, 4, 6 かつ 整数なので
b = 2, y = 2 ・・・⑤
b = 4, y = 1 ・・・⑥
③、④、⑤、⑥ の組み合わせより、
( a, b ) = ( 1, 2 ), ( 1, 4 ), ( 3, 2 ), ( 3, 4 )
となります。
問1 (2)
この問題は、かなり引っ掛けがきつい(というよりは、ずるい)問題です。入試問題としては首を捻ります。
①、②をそれぞれ、x = 0 を代入し、A、B の y 座標を求めます。
A (x , y ) = ( 0, 10 / b )
B ( x, y ) = ( 0, -( 2 / b ) )
より、辺AB = ( 10 / b ) – ( – ( 2 / b ) ) = 12 / b
b = 2, 4, 6 のいずれかなので、もっとも AB が小さくなるのは b = 6 の時で、
AB = 2 ・・・(ウ)
①、② の連立方程式を解いて、交点の x 座標 を求めると、
x = 6 / a となることから
a = 1, 3, 5 の中で最も x が小さくなるのは
a = 5 の時で、x 座標は 6 / 5 (イ) となります。
円の面積は、底辺 × 高さ × ( 1 / 2 ) より、
2 × ( 6 / 5 ) × ( 6 / 5 ) = 6 / 5 (ウ) となります。
解答・解説
ここでは、解答例のみの掲載となります。
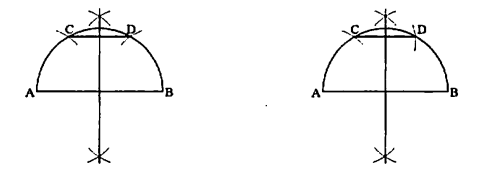
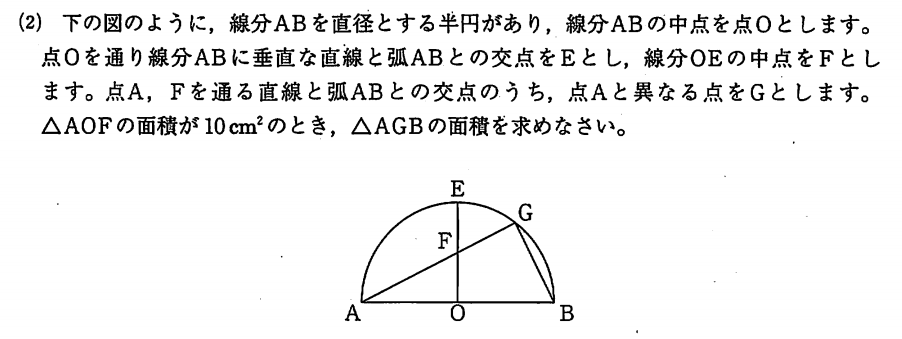
解答・解説
面積ならば相似です。また相似比が 1: 2 であれば、面積比は 1: 4 です。これは、覚えておきましょう。ちなみに体積比は 1 : 9 になります。
△AOF と △ AGB に着目します。
∠AOF = ∠ AGB = 90° ・・・①
∠OAF = ∠GAB は共通 ・・・②
①、② より、△AOF ∽ △ AGB
OA = OB = 1 とすると、OF = 1 / 2
三平方の定理より
AF2 = OF2 + OA2 = ( 1 / 2 )2 + 12 = 5 / 4
AF = √5 / 2 となります。
△AOF ∽ △ AGB の相似比は
AF : AB = ( √5 / 2 ) : 2 = √5 : 4
となります。
△AOF の面積 : △AGB の面積 = ( √5 )2 + 42 = 5 : 16 から
10 : x = 5 : 16
5x = 160
x = 32
よって、
△AGB の面積は、32 cm2 です。