ここでは、平成24年神奈川県高校入試数学の解説を行っています。
スポンサーリンク
問1

解答・解説
( ア ) -9 + 6 = -3
( イ ) 6 – 3 × ( 4 – 8 )
= 6 – 3 × ( -4 )
= 6 + 12
= 18
( ウ ) ( 1 / 3 ) – ( 5 / 8 )
= ( 8 – 15 ) / 24
= – 7 / 24
( エ ) 32a2b ÷ 8b
= 4a2
( オ ) ( 4x – 1 ) / 3 – ( 7x – 3 ) / 9
= 3 ( 4x – 1 ) / 9 – ( 7x – 3 ) / 9
= ( 12x – 3 ) / 9 – ( 7x – 3 ) / 9
= ( 12x – 3 -7x + 3 ) / 9
= 5x / 9
( カ ) √24 + 30 / √6
= 2 √6 + ( 30 √6) / 6
= 2 √6 + 5 √6
= 7 √6
( キ ) ( x + 2 )2 – ( x – 1 )( x + 6 )
= x2 + 4x + 4 – x2 – 5x + 6
= – x + 10
問2

解答・解説
( ア ) ( x – 6 ) ( x + 3 ) – 4x
= x2 – 3x – 18 – 4x
= x2 – 7x – 18
= ( x – 9) ( x + 2 )
( イ ) 2x2 – 5x + 1 = 0
解の公式を使います。
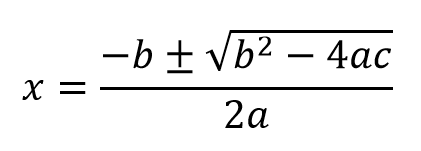
解の公式
x = ( 5 ± √17 ) / 4
( ウ ) 上に凸の2次関数であり、x = 0 のとき、y は最大値 0 となります。
x が 0 から離れるほど y の値は小さくなりので、x = 3 のとき y は最小となります。そのときの y の値は – 1 / 3 × 3 × 3 = -3 です。
よって、a = -3, b = 0
( エ ) 最も小さな自然数となる n を求めます。与えられた値を有理化すると、( 4√15n ) / 5 となります。
よって、n = 15 のときに自然数となることがわかります。
( オ ) 下の図のように補助線をひきます。
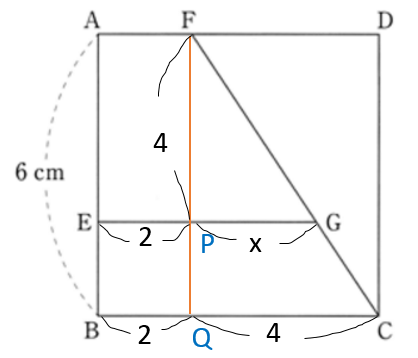
△FPG ∽ △FQC より、FP : FQ = PG : QC から
4 : 6 = x : 4 より、x = 8 / 3 = PG がわかります。
EG = 2 + PG なので、EG = 14 / 3 となります。
問3
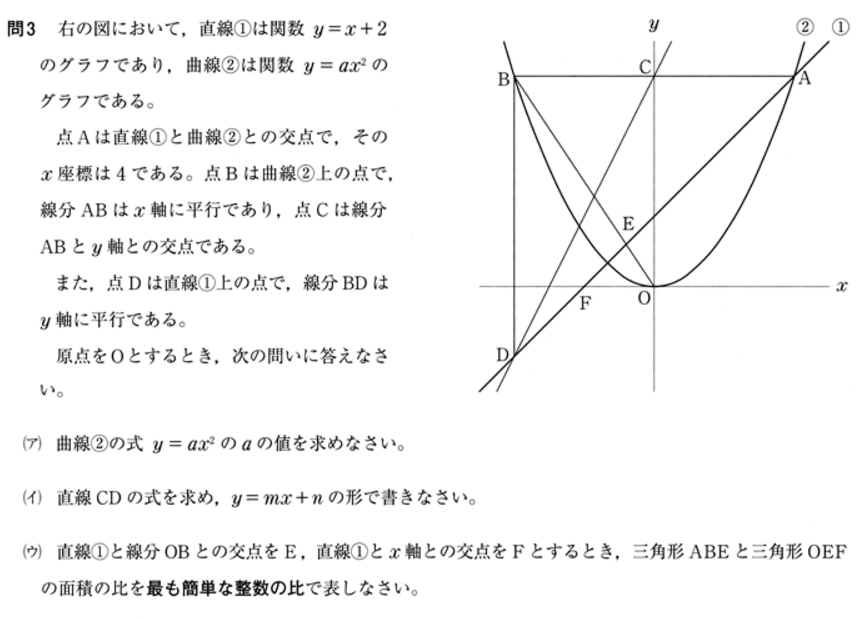
解答・解説
( ア ) 点A は y = x + 2 上にあり、x = 4 なので y = 6 であることがわかります。
点A ( 4, 6 )
また、点Aが曲線上の点でもあるので y = ax2 に代入して a を求めます。
6 = a × 4 × 4 より
a = 3 / 8
( イ ) 点C の座標は点C ( 0, 6 ) です。また、点D の x 座標は -4 であり、y = x + 2 上の点であることより、
点D ( -4, 2 ) であることがわかります。
2点CDの座標から CD の初期を求めます。計算は省略します。レッツトライ!
y = 2x + 6
( ウ ) OF を底辺とする △EOF と AB を底辺とする △EBA を考えます。
F の x 座標は y = x + 2 より 0 = x + 2 を計算して x = -2 がわかります。つまり OF = 2 です。
また、AB は 8 です。 これらのことから、底辺の比は 1 : 4 であることがわかります。
また、△EOF ∽ △EBA であることから、高さの比も 1 : 4 であることがわかりますので、
求める面積の比は、△EOF ∽ △EBA = 1 : 16
直線OB の式を求めて、①式との交点E の座標を実際に求めることもできます。また、高さの比が 1 : 4 であることが確認できます。
問4

解答・解説
( ア ) 袋M には4種類のカード、袋N には 8種類のカードがあるのでカードを取り出すパターンは 4 × 8 = 32 通りとなります。また、太郎さんと花子さんが同じ駅で降りるには、袋Mと袋Nのカードの数字の合計が 11である必要があります。合計が11となるパターンは以下の3パターンです。
| 袋M | 袋N |
|---|---|
| 4 | 7 |
| 7 | 4 |
| 10 | 1 |
よって求める確率は 3 / 32 です。
( イ ) 隣の駅で降りるには、袋Mと袋Nの数字の合計が 10, または 12 である必要があります。そうなる数字の組み合わせは以下のように5パターンです。
| 袋M | 袋N |
|---|---|
| 4 | 6, 8 |
| 7 | 3, 5 |
| 10 | 2 |
よって求める確率は 5 / 32 です。
問5
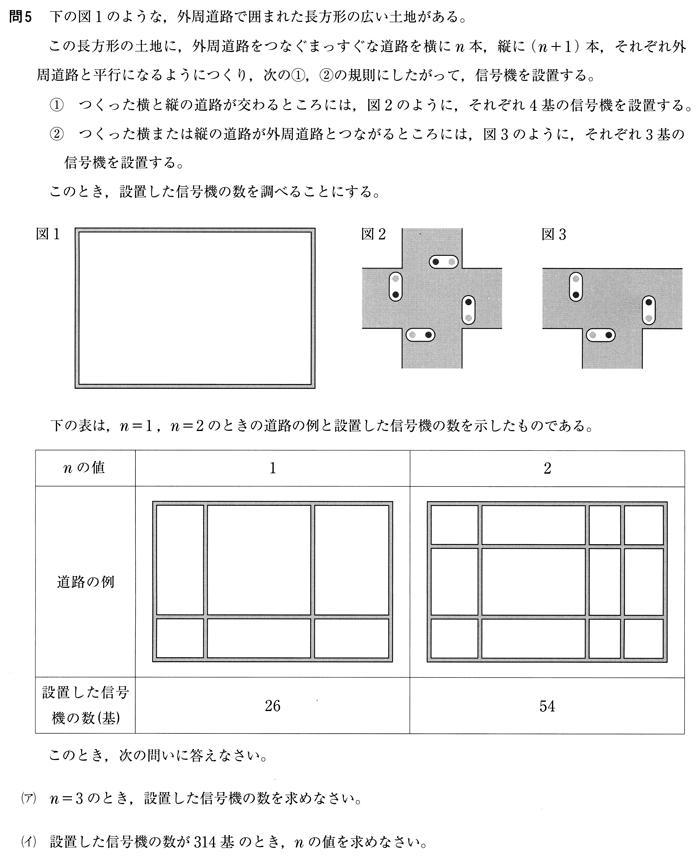
解答・解説
( ア ) n = 3 のとき、設置した信号機を求めるには実際に線をひいて信号機4つの交差点の個数と信号機3つのT字路の数を数えればすぐにもとまります。
まずは、n = 1, n = 2 のときのケースから n と 交差点の数とT字路の個数の関係を求めてみます。
| n | T字路 ( 信号3つ ) の数 | 交差点 ( 信号4つ ) の数 |
|---|---|---|
| 1 | 6 | 2 |
| 2 | 10 | 6 |
| n | 2n + 2(n + 1) = 4n + 2 | n × (n + 1) |
この関係を求めることが出来れば、n = 3 を代入して
T 字路の数 ( 信号機3つ ) = 4 × 3 + 2 = 14
交差点の数 ( 信号機4つ ) = 3 × ( 3 + 1 ) = 12
がわかりますので、設置する信号機の合計は 14 × 3 + 12 × 4 = 90 より、
信号機の数は 90 基 となります。
( イ ) 設置した信号機が 314 基であることから、以下の方程式が成立します。
3 ( 4n + 2 ) + 4 n ( n + 1 ) = 314
12n + 6 + 4n2 + 4n = 314
4n2 + 16n – 308 = 0
n2 + 4n – 77 = 0
( n + 11 ) ( n – 7 ) = 0
n > 0 なので、
n = 7 となります。
問6
解答・解説
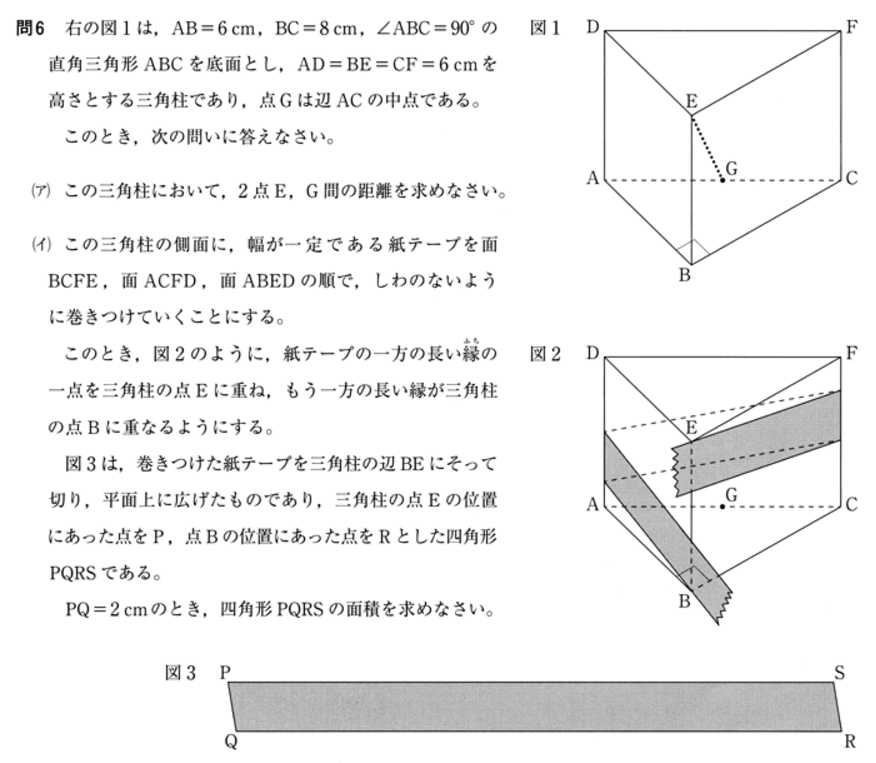
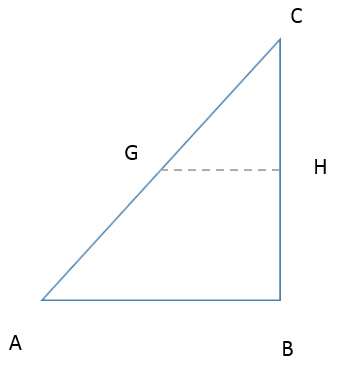
( ア ) EG の距離を求めます。△ ABC に着目して、下の図のように BC の中点を H とし、GH を結びます。
AB = 6, BC = 8, ∠B = 90° より三平方の定理から
AC2 = AB2 + BC2 = 62 + 82 となり、
AC = 10 が求まります。また、中点連結定理より BH = HC = 4, AG = GC = 5, GH = 3 が求まります。
次は、△ EBH に着目します。
△ EBH は∠B = 90° の直角三角形なので、三平方の定理から
EH2 = EB2 + BH2 = 62 + 42 となり、
EH2 = 52 となります。
次は、△ EGH に着目します。
△ EGH は∠H = 90° の直角三角形なので、またまた三平方の定理より
EG2 = EH2 + HG2 = 52 + 32 = 61 がわかります。
よって EG = √61 cm となります。
中点と問題文にある場合は、中点連結定理をまずは疑いましょう。また、△ABC のように辺の比が 3:4:5 の場合は直角三角形です。これも覚えておきましょう。何かと便利です。
( イ )
この問題は、発想の転換ができればあっという間に解けます。三角柱の展開図を見てみましょう。
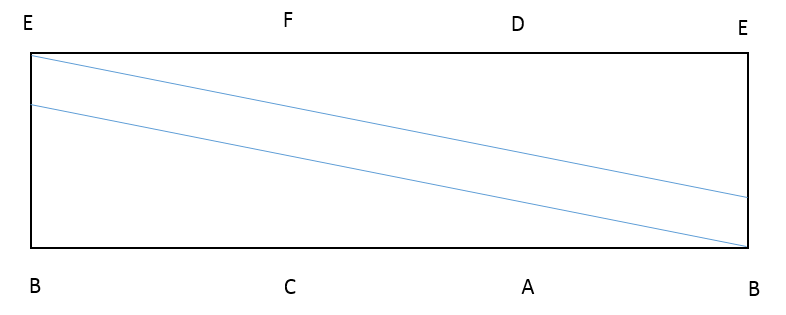
もうお気づきだと思いますが、直接的に平行四辺形の面積を求めようとするのではなく、長方形から三角形の面積を減算して、平行四辺形の面積を求めます。
長方形の縦の長さ = EB = 6 cm
長方形の横の長さ = BA + AC + CB = 6 + 10 + 8 = 24 cm
長方形の横の長さを三角形の底辺とすると、
三角形の高さ = AB – PQ = 6 – 2 = 4 cm
となります。
これらから、平行四辺形 PQRS の面積を計算すると、
48 cm2
が求まります。
この問題で最も驚くべきことは、三角柱に紙テープをきっちり最短経路で貼った人です。まさに匠の技です。
問7

解答・解説
( ア )
ナビに従って回答する問題です。知識を問う問題となりますので、単語を覚えておく必要があります。
( ⅰ ) 対頂角
( ⅱ ) ∠ADB = ∠BAC
( ⅲ ) 2組の角がそれぞれ等しい
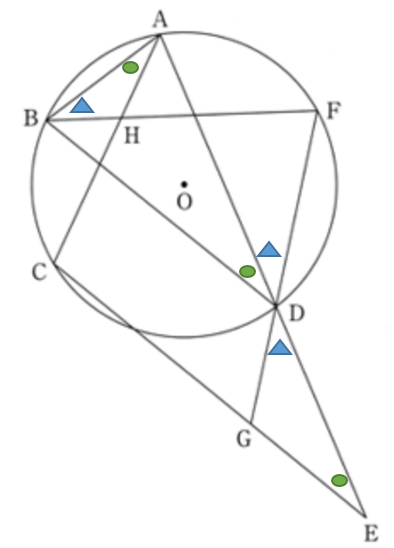
図で表すと下の図のようになります。
( イ )
∠ADF = 35°, ∠DBF = 41° のときの ∠ACE を求めます。まず、下の図に示すように、BD と AC の交点を P とします。
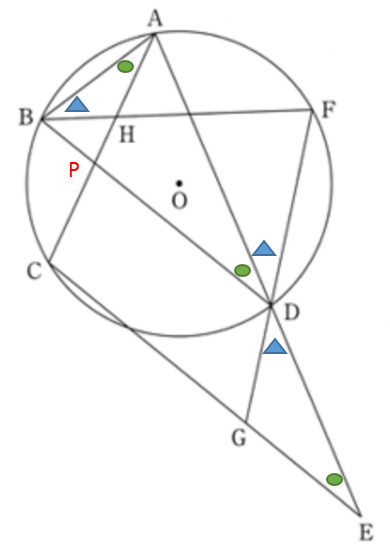
問題文より、∠ABF = 35°、∠DBF = 41° より、∠ABD = 35 + 41 = 76° です。
△ABD は BD = AD の二等辺三角形であることから、∠BAD = 76° であることがわかります。
よって、∠BDA = 180 – ( 76 × 2 ) = 28° となります。
∠APD = ∠ABP + ∠PAB = 28° + 41° + 35° = 104° ・・・①
BD // CE ・・・②
①、②より、
∠APD = ∠PCE ( 同位角 )
なので、
∠ACE = 104° となります。