[ 高校数学 ] 1rad.(ラジアン)の定義 ～度との相互変換～

角度を表す場合に、1ラジアンとか1度とかっていいますが一体定義はどうなっているのでしょうか？

1度の定義はわかりますよね。円を 360分割した角度です。では、1ラジアンの定義はどうなっているのでしょうか？以下の図を見てみてください。

1ラジアンの定義

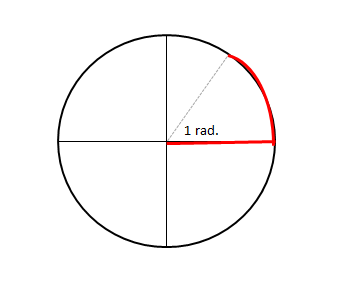
1rad の定義は上図のようになっています。半径と弧の長さが等しくなるような扇形の角度です。三辺の長さが等しい正三角形ならぬ正扇形とでも呼べそうな形です。そして角度で言うと、57.2958度くらいです。いきなり 1rad は 57.29度と言いましたが、どのように計算できるのでしょうか？以下の式は覚えていますでしょうか？

円周 = 直径　×　円周率

つまり半径をrとする円の円周は、2πr です。つまり、半径に 2π をかけると円の円周が計算により求めることができます。このことより円を１周したとき(360度に相当)のラジアンは 2π ラジアンということがわかります。

円を半分だけ進んだら(180度に相当)、π ラジアン、90度であれば、( π / 2 ) ラジアンと言うことになります。

では、比率で 1rad が何度になるか計算してみます。

180度　：　π ラジアン　＝　x 度　：　１ラジアン

πx　＝　180

ｘ　＝　180　/　π

ｘ　≒　180　/　3.14

x　≒　57

いかがでしたでしょうか。上記の計算結果より、１ラジアンは大体57度であることがわかります。1 rad の計算方法は理解できたでしょうか。

ラジアンと度を変換する公式

ラジアンと度を相互変換するには次の公式を使って計算することができます。

• 角度 = ラジアン x 180 / 円周率(π)
• ラジアン = 角度 x 円周率(π) / 180