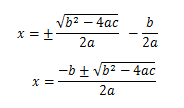ここでは、中学生で学習する 2 次方程式の解の公式を導出してみようと思います。公式を覚えて問題を解くのはもちろん間違いではありませんが、必ずその公式を導いた人がいます。紀元前には、世界各地でその解法は既知だったようです。
スポンサーリンク
解の公式
まずは、解の公式です。覚えていますよね?
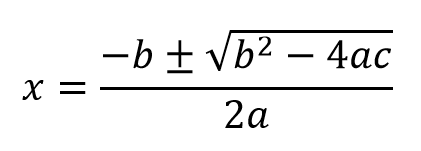
解の公式
ここでは、解の公式を自分で導出できるようになることが目標です。
解の公式を導出する基本的な考え方
まずは、どのような考え方をもとに解の公式を求めるかを示します。
ここでは、この考え方を基準に導出してみようと思います。なお、( px + q )2 の形に変形することを平方完成と言います。
2次方程式の解の公式を導出する
では、平方完成目指していきましょう。
ここまできたら、もう少しでいつも目にしている解の公式を導けます。
これで、2次方程式の解の公式を導出することができました。
解の公式からわかること
解の公式を導出することができましたが、この結果から以下のことがわかります。
- ある数を 0 で割ることはできないので a ≠ 0
- 根号の中は 0 以上である必要があるので b2-4ac ≧ 0
なお、2次方程式の解の個数は、下表の通りになります。
| 条件 | 解の個数 |
|---|---|
| b2-4ac > 0 | 実数解が2つ |
| b2-4ac = 0 | 実数解が1つ |
| b2-4ac < 0 | 実数解なし |