平成27年千葉県高校入試の数学前期選抜試験の問題番号3 ~ 5 の解答・解説を掲載しています。
スポンサーリンク
問題番号3
下の図1のように、関数 y = ax2 のグラフと直線 y = x + 4 の交点を B, D, 関数 y = ax2 のグラフと直線 y = ( -1 / 2 )x + 3 の交点を A, C, 直線 y = x + 4 と直線 y = ( -1 / 2 )x + 3 を E とする。4点 A, B, C, D の x 座標が、それぞれ -3, -2, 2, 4 であるとき、次の (1), (2) の問いに答えなさい。ただし、a > 0 とする。また、原点 O から点 ( 1, 0 ) までの距離及び原点 O から点 ( 0, 1 ) までの距離をそれぞれ 1 cm とする。
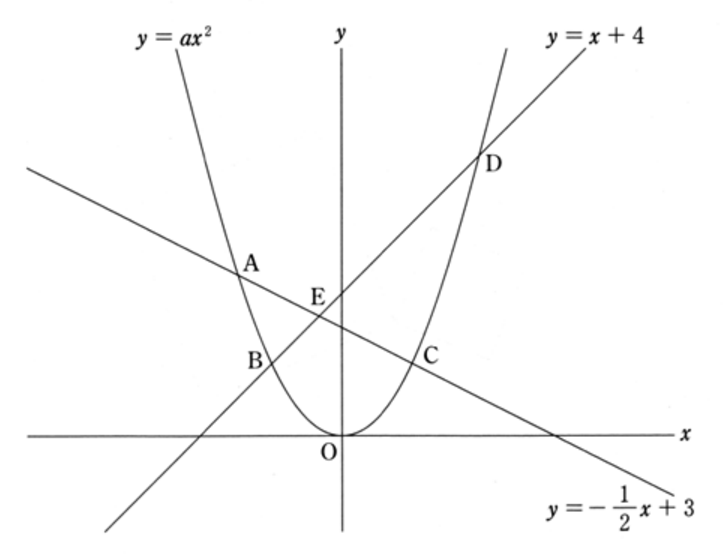
図1
(1) a の値を求めなさい。
解答・解説
問題文も長く、点もわんさか登場しますが、落ち着いて、まずは与えられていること・わかることを整理してみましょう。まずは、点 A, B, C, D の x 座標はすべて与えられていますので、y 座標も直線の式に代入することで計算できます。
点 A ( -3, 9 / 2 )
点 B ( -2, 2 )
点 C ( 2, 2 )
点 D ( 4, 8 )
これらはすべて、y = ax2 を通る点なので、このうちの1点を2次関数 y = ax2 に代入して a を求めます。ここでは、点C を使用します。
2 = a × 2 × 2 から
a = 1 / 2 であることがわかります。
(2) 下の図2は、図1において、x 軸上に点 P をとり、点 P を通る y 軸に平行な直線 ℓ をひいたものである。この直線 ℓ が、関数 y = ax2 のグラフ、直線 y = x + 4、直線 y = ( -1 / 2 )x + 3 と交わる点のうち、y 座標が最も大きい点を Q 、最も小さい点を R とするとき、次の①、②の問いに答えなさい。
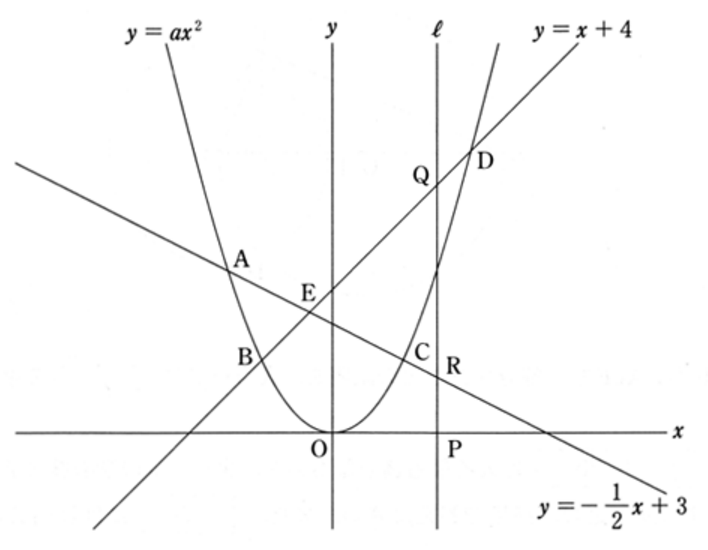
図2
① 直線 ℓ が点 E を通るとき、線分 QR の長さを求めなさい。
解答・解説
直線 ℓ は y 軸と平行にひいたことはわかりますが、どうやら y 軸に平行なまま動くようです。問題文が不親切ですね。さて、気を取り直して問題を見てみたいと思います。
図2 をみると、直線 ℓ が点 E にくるときは、点 E と 点 Q は等しく、点 R は2次関数上との交点であることがわかります。まず点 E の座標を求めます。直線 y = x + 4、直線 y = ( -1 / 2 )x + 3 との交点ですので、
x + 4 = ( -1 / 2 )x + 3 から x を求めると、x = -2 / 3 となり、y = 10 / 3 がわかります。
点 Q = 点 E ( -2 / 3, 10 / 3 )
点 R の y 座標は y = ( 1 / 2) x2 の x = -2 / 3 のときの値なので
点 R ( -2 / 3, 2 / 9 ) が求まります。線分 QR の長さは点 Q と 点 R の y 座標の差になることから、
( 10 / 3 ) – ( 2 / 9 ) = ( 28 / 9 ) cm です。
② -3 ≦ x ≦ 4 のとき、線分 QR の長さが 3 cm となる点 P の x 座標をすべて求めよ
解答・解説
何度もいいますが、問題文が気になります。せめて、「直線 ℓ が -3 ≦ x ≦ 4 の範囲を動くとき・・・」のような問題文にはならないものでしょうか。
直線 ℓ の位置によって、点Q, R となるグラフが変わってきますので場合分けして下表のようにまとめました。
| x 軸の範囲 | 点Q をもつ関数・直線 | 点R をもつ関数・グラフ |
|---|---|---|
| 点AB間 ( -3 ≦ x < -2 ) | 直線 y = ( -1 / 2 )x + 3 | 直線 y = x + 4 |
| 点BE間 ( -2 ≦ x < -2 / 3 ) | 直線 y = ( -1 / 2 )x + 3 | y = ( 1 / 2) x2 |
| 点EC間 ( -2 / 3 ≦ x < 2 ) | 直線 y = x + 4 | y = ( 1 / 2) x2 |
| 点CD間 ( 2 ≦ x ≦ 4 ) | 直線 y = x + 4 | 直線 y = ( -1 / 2 )x + 3 |
それぞれの区間において、y 座標の差分 ( 点 Q - 点 R ) を求めます。
点AB間
{ ( -1 / 2 )x + 3 } – { ( x + 4 ) } = ( -3 / 2 )x -1 となります。
( -3 / 2 )x -1 = 3 となる x を求めると、x = -8 / 3 となります。 ( -3 ≦ x < -2 ) の条件も満たしているので、求める解答の1つです。
点BE間
{ ( -1 / 2 )x + 3 } – { ( 1 / 2) x2 } = 3 の方程式を解くと
x ( x + 1 ) となり、x = 0, -1 となります。 ( -2 ≦ x < -2 / 3 ) の条件を満たすのは x = -1 だけなので、x = 0 は除外します。
残りの区間も同様に解いていき、x の範囲の条件を満たすものすべてが解答となります。残りの区間に答えがあるかないかは、各自で確認してみましょう。
問題番号4
下の図のように、点 O を中心とし、線分 AB を直径とする円 O がある。線分 OB 上に、2点 O, B と異なる点 E をとり、点 B を中心とし、線分 BE を半径とする円 B をかく。2つの円の交点をC, D とし、点 C から線分 AB に垂線 CF をひく。また、点 C と、点 A、点 B、点 E をそれぞれ結ぶ。このとき、次の (1) (2) の問いに答えなさい。
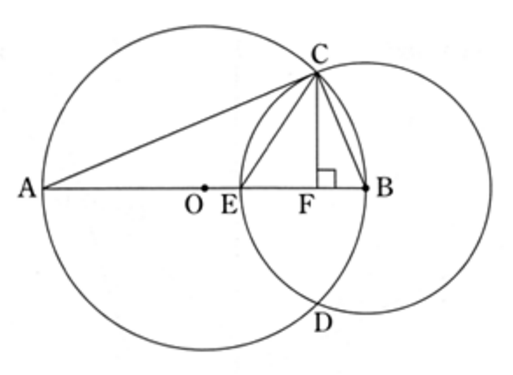
(1) 線分 CE が ∠ ACF を二等分することの証明を、途中まで示してある。(a) (b) に入る最も適当なものを、選択肢の ア ~ カ のうちから、それぞれ1つずつ選び符号で答えなさい。また、証明の続きを完成させなさい。
選択肢 ア:∠AEC イ:∠ACB ウ:∠BAC エ:∠ABC オ:∠BCF カ:∠BCE
解答・解説
以下に解答例を載せておきます。(a) (b) を選択肢から選び、太字の部分はすべて回答者が記述しなければいけない部分です。証明の出だしの部分はナビゲートされています。ゆっくり確認してみましょう。
証明
△ CFB と △ ACB において、
共通な角だから、∠CBF = (a) エ ・・・ ①
仮定と、線分 AB は円 O の直径であることから、
∠CFB = (b) イ = 90° ・・・ ②
①、②より、2組の角がそれぞれ等しいので、
△ CFB ∽ △ ABC ・・・③
③より、∠BCF = ∠BAC ・・・④
円の半径から、BC = BE ・・・⑤
⑤より、△BCE は、BC = BE の二等辺三角形なので、
∠BCE = ∠BEC ・・・⑥
△CAE において、1つの外角は、これととなりあわない2つの内角の和に等しいので、
∠BEC = ∠CAE + ∠ACE
よって、∠ACE = ∠BEC - ∠CAE = ∠BEC - ∠BAC ・・・⑦
また、∠ECF = ∠BCE - ∠BCF ・・・⑧
④、⑥、⑦、⑧より、∠ACE = ∠ECF
従って、線分CEは∠ACF を二等分する。
(2) 円B の半径が 1cm で、△CFB と △ACB の面積比が 1:16 のとき、線分 CE の長さを求めなさい。
解答・解説
この問題のポイントは、△ CFB ∽ △ ABC であることを利用します。面積比が1:16であるということは、辺の長さは△ CFB と△ ABC では 1:4 になります。また、円 B の半径が 1cm なので、線分 CB = BE = 1cm ということがわかります。ここからスタートです。
線分FB の長さを求めます。△ CFB ∽ △ ABC なので、辺の長さの比は 1:4 であることから、FB は BC の 1 / 4 の長さであることがわかります。BC = 1cm なので、FB = ( 1/ 4 ) cm です。次に BE = 1cm なので、EF = 1-( 1 / 4 ) = 3 / 4 であることもわかります。
△ CFB に着目します。直角三角形なので、三平方の定理から、CF の長さを求めることができます。計算すると、CF = ( √15 / 4 ) になります。計算はがんばってしてみてください。
次に、△ CFE に着目します。こちらも直角三角形なので、EF と CF の長さより、三平方の定理より CE の長さを求めることができます。
結果は、CE = ( √6 / 2 ) cm になります。
おじさん、悩みました。
問題番号5
下の図1のように、1目盛りが、縦横ともに 1cm の等しい間隔で線がひかれている方眼紙の、縦線と横線の交点に点( ・ ) が打ってある。この点のうちから、2点A, B をAB = 4 cm となるようにとる。さらに、点 C を∠CAB = 90° 、AC = n cm ( n は正の整数 ) となるようにとり、3点A, B, C を結んで直角三角形をかいたとき、直角二等辺三角形 ABC の内部及び周上にある点の個数を N とする。次のはるかさんと先生の会話を読み、(1) ~ (3) の問いに答えなさい。
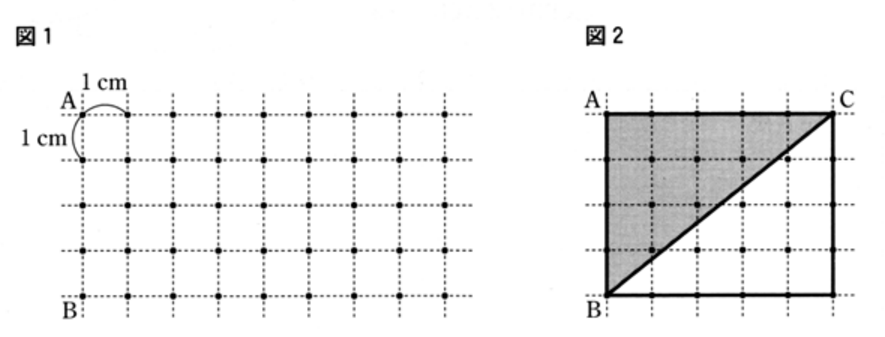

(1) 会話中の ( ア ) ~ ( エ ) に入る数をそれぞれ書きなさい。
解答・解説
( ア ) ~ ( エ ) については、実際に線をひいて確認すればよいでしょう。
- n = 3 のときは、点B, C 上の点2個 N = 11
- n = 4 のときは、点B, C 上の点5個 N = 15
- n = 5 のときは、点B, C 上の点2個 N = 16
- n = 6 のときは、点B, C 上の点3個、N = 18
- n = 7 のときは、点B, C 上の点2個、 N = 21
- n = 8 のときは、点 B, C 上の点5個、N = 25
ここから ( ア ) 3 ( イ ) 3 ( ウ ) 5 ( エ ) 25 がわかります。
(2) 辺 BC 上にある点の個数が最も大きくなる場合の n と N の関係について考える。このとき、N を、n を使った式で表しなさい。
解答・解説
辺 BC 上にある点の個数が最も大きくなる場合の関係性です。最も大きくなるのは5個です。よって、以下の条件から関係を考えます。
- n = 4 のときは、点B, C 上の点5個 N = 15
- n = 8 のときは、点 B, C 上の点5個、N = 25
なんとなく、比例の関係があるように思いますので、同一直線状の N = an + b を考えて連立方程式を解いて見ます。
連立方程式
15 = 4a + b ・・・①
25 = 8a + b ・・・②
これらを解くと、a = 5 / 2, b = 5 となります。従って、( 2点では頼りないですが)
N = ( 5 / 2 ) n + 5
の関係性が求めることができます。
(3) 辺 BC 上にある点の個数が最も少なくなる場合の n と N の関係について考える。このとき、 N = 186 であるような n の値を求めなさい。
解答・解説
点BC 上にある点の個数が最も少ないのは、2個のときです。そのときの n と N は以下のようになっていることはわかっています。
- n = 3 のときは、点B, C 上の点2個 N = 11
- n = 5 のときは、点B, C 上の点2個 N = 16
- n = 7 のときは、点B, C 上の点2個、 N = 21
今度は3点ありますので、バッチリ関係性が求められますね。まず n はどうやら奇数の場合にBC 上の点が2個となるようです。また、そのときの増える割合は 5 であることがわかります。先ほどと同じように連立方程式を解いてみます。
連立方程式
16 = 5a + b ・・・①
21 = 7a + b ・・・②
これらを解くと、a = 5 / 2, b = 7 / 2 となります。従って、
N = ( 5 / 2 ) n + ( 7 / 2 )
の関係式が求まります。
N = 186 のときの n を求めると、n = 73 となります。