平成27年千葉県高校入試の数学前期選抜試験の問題番号1 と 2 の解答・解説を掲載しています。
スポンサーリンク
1.次の(1) ~ (6) の問に答えなさい。
(1) ( -7 ) – ( -4 ) を計算しなさい
= -7 + 4 = -3
(2) ( -4 )2 + 8 ÷ ( -2 ) を計算しなさい
= 16 – 4
= 12
(3) ( 3a -2b ) / 2 – ( 2a – b ) を計算しなさい
= 3a / – b – 2a + b
= -a / 2
(4) 等式 2a -3b = 1 を b について解きなさい。
3b = 2a -1
b = ( 2a – 1 ) / 3
(5) √32 – 2√18 + 5√2 を計算しなさい
= 4√2 – 6√2 + 5√2
= 3√2
(6) 二次方程式 x2 -2x = 3( x – 1 ) を解きなさい
x2 – 2x = 3x – 3
x2 – 5x + 3 = 0
因数分解できそうもないので、解の公式を使って解きます。必ず覚えておきましょう。
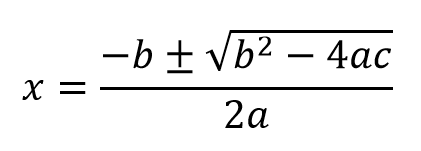
解の公式
公式を使って解くと、
x = ( 5 ± √13 ) / 2
となります。
2.次の(1) ~ (5) の問いに答えなさい。
(1) 下の図は、あるクラスの生徒20人が冬休み中に読んだ本の冊数を、ヒストグラムに表したものである。この20人が読んだ本の冊数について述べた文として適切なものを次の ア ~ エ のうちから1つ選び、符号で答えなさい。
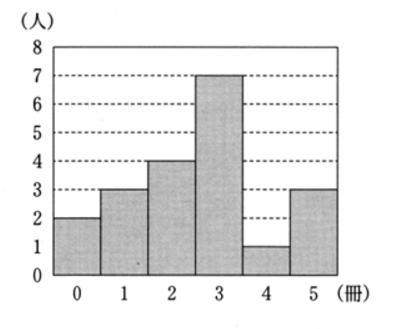
ヒストグラム
ア 分布の範囲(レンジ)は、4冊である
イ 最頻値(モード)は、5冊である
ウ 中央値(メジアン)は、3冊である
エ 平均値は、2.3冊である
解答・解説
では、ア から順に見ていきましょう。
分布の範囲は0冊から5冊です。4冊ではありません。従って ア は間違いです
最頻値は5冊ではありません。一番グラフが高くなっている部分ですので最頻値は3冊です。従って イ も間違いです。最頻値とは最も頻繁に出てくる値のことです。
中央値は、データを小さいほうから大きいほう(その逆でもOK)に並べたときの真ん中のデータのことです。今回は20人いますので、データを小さいほうから並べて10番目にくる値のことです。0冊が2人、1冊が3人、2冊が4人ですので、ここまでで 8人分のデータとなります。10番目のデータは3冊の中にあることがわかりますので、中央値は3冊です。従って ウ は正しいです。
エ は間違いが確定していますが確認してみます。まずは、全員で何冊読んだのか合計を出します。
0冊 × 2人 + 1冊 × 3人 + 2冊 × 4人 + 3冊 × 7人 + 4冊 × 1人 + 5冊 × 3人
計算すると、全員で51冊読んでいることがわかります。20で割って平均を求めると 2.55 冊になりますので、エ は間違いであることがわかります。
(2) n を50以下の正の整数とする。![]() が整数となるような n の個数を求めなさい。
が整数となるような n の個数を求めなさい。
解答・解説
n は50以下の正数であるので、根号(ルート)内の 3n は150 以下であることがわかります。次にルートが正数になるには、3n はある値の2乗である必要があります。では、150以下である値の2乗となる数値を洗い出してみましょう。
1 × 1 = 1
2 × 2 = 4
3 × 3 = 9 = 3 × 3
4 × 4 = 16
5 × 5 = 25
6 × 6 = 36 = 3 × 12
7 × 7 = 49
8 × 8 = 64
9 × 9 = 81 = 3 × 27
10 × 10 = 100
11 × 11 = 121
12 × 12 = 144 = 3 × 48
この数値の中から赤字で示した 3の倍数のものが根号が外れる n (3, 12, 27,48 ) になります。その個数は4つです。
(3) 下の図の△ ABC を、辺 AC を軸として1回転してできる立体の体積を求めなさい。ただし、円周率は π を用いることとする。
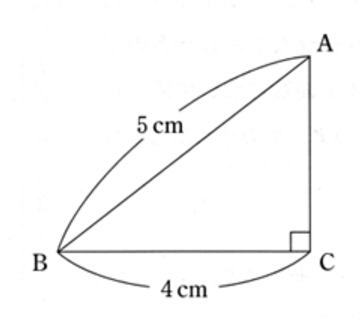
解答・解説
辺 AC を軸に1回転させてできる立体は円錐です。ピラミッドみたいなものではありませんよ。この問題の場合では、底面の半径が 4cm で高さが AC の円錐になります。よって体積を求めるには 辺 AC の長さを求めなくてはいけません。三平方の定理より、
AB2 = AC2 + BC2
からAC は 3 であることがわかります。よって求める円錐の体積は、
( 42π × 3 ) / 3 = 16π cm3 です。
(4) 下の図のように、点 A , B, C, D, E, F, G. H を頂点とする立方体があり、この頂点上を移動する2点 P, Q がある。大小2つのサイコロを同時に1回投げる。点 P は、点 A を出発点として、大きいサイコロの出た目の数だけ、⇒ B ⇒ C ⇒ D ⇒ A ⇒ B ⇒ C の順に移動し、点 Q は、点 E を出発点として、小さいサイコロの出た目の数だけ、 ⇒ H ⇒ G ⇒ F ⇒ E ⇒ H ⇒ G の順に移動する。このとき、直線 PQ と直線 CG が、ねじれの位置にある確率を求めなさい。ただし、サイコロを投げるとき、1から6までのどの目が出ることも同様に確からしいものとする。
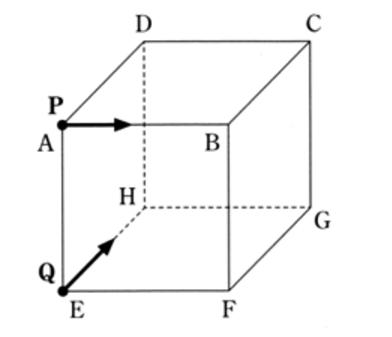
解答・解説
面倒そうな問題ですが、P は上をグルグル、Q は下をグルグル回るだけのようです。まず、サイコロの振ったときに出る目のパターンは 6 × 6 の 36 通りです。
次に CG とねじれの位置にある線を考えます。P は立方体の上を、Q は立方体の下を回るので、AB はCG とねじれの位置にありますが PQ がそうなることはありません。PQ がなりうるねじれの位置は以下の直線です。
CG とねじれの位置にある直線 : AH、AF、BH、BE、DF、DE
下表にねじれの位置になるときのサイコロの出た目をまとめます。
| 直線PQ | P 大きなサイコロの目 | Q 小さなサイコロの目 |
|---|---|---|
| AH | 4 | 2, 5 |
| AF | 4 | 3 |
| BH | 1, 5 | 1, 5 |
| BE | 1, 5 | 4 |
| DF | 3 | 3 |
| DE | 3 | 4 |
すべてのパターンは11通りであることがわかりますので、求める確率は 11 / 36 となります。
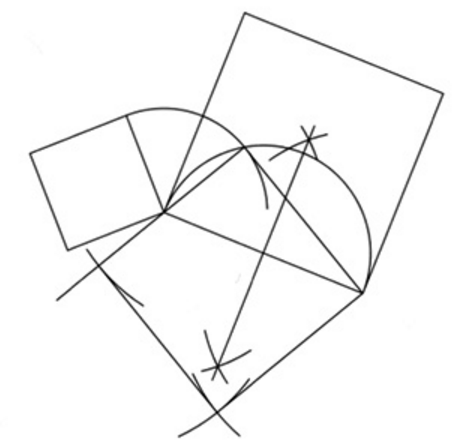
(5) 下の図のように、一辺の長さが異なる2つの正方形があり、1つの頂点が重なっている。このとき、面積が、2つの正方形の面積の差に等しい正方形を作図しなさい。ただし、三角定規の角を利用して直線をひくことはしないものとする。また、作図に用いた線は消さずに残しておくこと。
解答・解説