平成27年度北海道高校入試数学の学校裁量問題の解説を掲載しています。
スポンサーリンク
問1 大小2つのサイコロを同時に投げ、下の図に、ルールⅠまたはルールⅡに従って点 P をとります。点 O は原点とします。次の(1)、(2)に答えなさい。
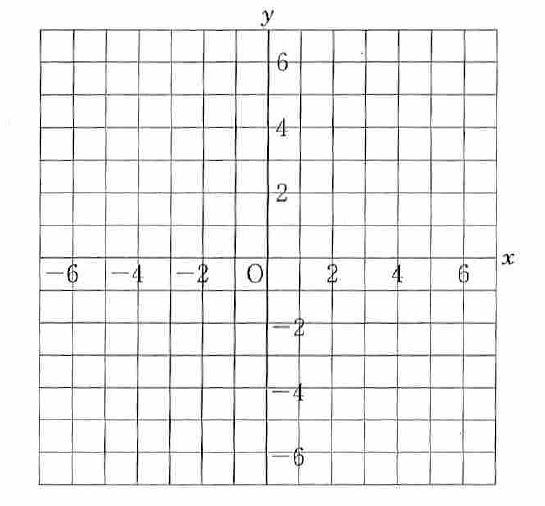
( ルールⅠ )
点 P の x 座標は、大きいサイコロの出た目の数とし、点 P の y 座標は、小さいサイコロの出た目の数とします。例えば、大きいサイコロの出た目の数が 1、小さいサイコロの出た目が 2 のとき、点 P は ( 1, 2 ) となります。
(1) ルールⅠに従うとき、点 P が関数 y = 6 / x のグラフ上の点になる確率を求めなさい。
まず、サイコロの出るパターンは36通りであることを頭に入れておきましょう。大小それぞれのサイコロは 1 ~ 6 の6通りであり、6 × 6 の36パターンです。
次に ルールⅠを適用する場合には、x および y 軸が正のエリアだけを考えることになります。x も y も負の数になることはありません。また、x も y も小数になることはありません。
これらのことより y = 6 / x の反比例のグラフ上に点 P がくるパターンは、全部で
( x, y ) = ( 1, 6 ), ( 2, 3 ), ( 3, 2 ), ( 6, 1 )
の 4パターンであることがわかります。
よって確率は 4 / 36 = 1 / 9 となります。
( ルールⅡ )
点 P の x 座標は、大きいサイコロの出た目の数が偶数ならばその数とし、奇数ならばその数の符号を負とした数とします。また、点 P の y 座標は、小さいサイコロの出た目の数が偶数ならばその数とし、奇数ならばその数の符号を負とした数とします。例えば、大きいサイコロの出た目の数が 1、小さいサイコロの出た目が 2 のとき、点 P は ( -1, 2 ) となります。
(2) ルールⅡに従うとき、点 P と点 ( 1 / 2, 1 / 2 ) との距離が5以下になる確率を求めなさい。
次は多少複雑です。x も y も負の数となる場合があります。では、点 ( 1 / 2, 1 / 2 ) との距離が5以下ということはどのようなことを表しているのかを考えて見ます。下の図を見て下さい。
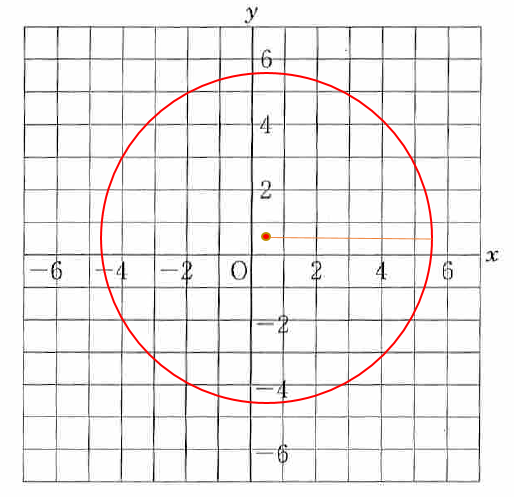
この図より、点( 1 / 2, 1 / 2 ) を中心にした半径5の円の中に点 P が入っているかと言うことです。後はルールに従って点P をプロットしていくと、円の中に入るパターンを割り出すことができます。 コンパス等で綺麗に円を描ければ微妙な部分がどちらかはわかると思います。または、範囲に入っているか微妙な場合には、三平方の定理から、点 ( 1 / 2, 1 / 2 ) との距離を計算して5以下であるかを検算することもできます。
大きなサイコロが 1 のとき x = -1 となりますから、x = -1 の縦線を見ていきます。このとき小さなサイコロが1 ~ 6 までのパターンを見ると、円の中に入るのは、
( x, y ) = ( -1, -1 ), ( -1, 2 ), ( -1, -3 ), ( -1, 4 ) の4パターンです。( -1, -5 ) ( -1, 6 ) は円の外であることがわかります。
あとは順に x = 2, x = -3, ・・・ を確認して、x と y の組み合わせをすべて数えると、合計で 16パターンあることがわかります。やってみましょう。
よって、確率は 16 / 36 = 4 / 9 となります。
問2 下の図のように、OA = 5 cm の直角二等辺三角形 OAB があります。次の(1) ~ (3) に答えなさい。ただし、円周率は π を用いなさい。
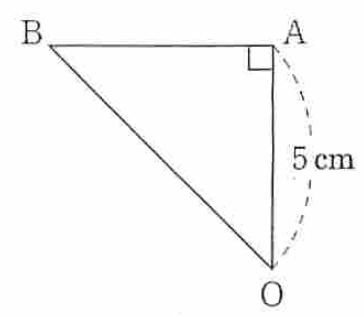
図1
(1) 図1 の△ OAB を、点 O を中心として矢印方向に 20° 回転させるとき、点 B が動いてできる弧の長さを求めなさい
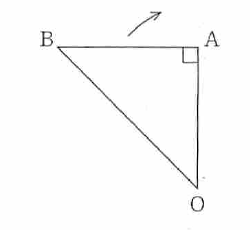
20°回転する
この問題は図形に惑わされてはいけません。OB だけに着目します。すると、点O を中心に半径 OB の円が 20° 分だけ描かれることがわかります。OA = AB = 5cm の二等辺三角形から OB は 5√2 であることはすぐにわかります。
従って、点Bが動いてできる弧の長さは、円周 × ( 20 / 360 ) で計算できます。
円周 = 2π × 半径 ( OB ) = 10π√2 より、
点Bが動いてできる弧の長さは、( 5√2 π / 9 ) です。
(2) 図1の△ OAB を、点 O を中心として矢印方向に 90° 回転させるとき、辺 AB が動いてできる図形の面積を求めなさい
90° 回転する
90° 回転すると AB はどのような軌跡となるのかイメージできるようになることができなければ、この問題は解けないでしょう。以下に AB の軌跡を図にしてみましたので、確認しましょう。図はかなりいい加減です。すいません。
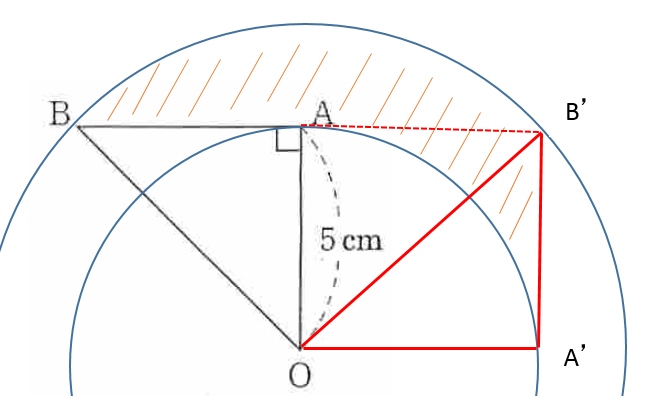
AB の軌跡
点O を中心に 90° 回転すると 点 A ⇒ 点 A’ 、点 B ⇒ 点 B’ にそれぞれ半径の異なる円を描いて移動します。まずは、この図を作成できるようにトレーニングしましょう。また、求める面積は斜線の部分の面積であることがわかります。
ここまでイメージできればほとんど解答できたも同じです。あとは、単純な計算だけです。斜線部の面積は B, A, B’ を通る直線より上の部分と下の部分をそれぞれ求めて合計を出します。
上の部分 : ( 中心 O と弧 BB’ の扇形の面積 ) - ( △ OBB’ の面積 )
下の部分 : ( 正方形 OAB’A’ ) - ( 中心 O と弧 AA’ の扇形の面積 )
扇形の中心角度は 上下ともに 90° になります。
この計算を行うと、最終的に求める面積は、25 π / 4 cm2 となります。
(3) 図2 のように、図1の△OABの辺OAと平行で、距離が 5 cm の直線 ℓ があります。△ OAB を、辺 OA を軸として 1回転させてできる立体を P、直線 ℓ を軸として 1回転させてできる立体を Q とします。立体 P の体積を求めなさい。また、立体 P の体積は、立体 Q の体積の何倍ですか、求めなさい。
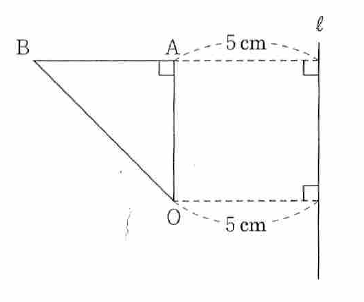
図2
立体 P が円錐になることがわかれば、立体 P の体積は簡単に求めることができます。底面が半径 5 cm の円で高さ 5 cm ( OA ) の円錐の体積になりますので、立体 P の体積は
1 / 3 × 5 × 5 × π × 5 = 125 π / 3 cm3 になります。
続いて 立体 Q の体積ですが、立体 P と底面が半径 5 cm の円, 高さ 5 cm の円柱の体積の合計となります。体積を計算しても良いですが、立体 P は 立体 Q の何倍の体積かを問題では問われています。
立体 Q の円柱部分の体積は 立体 Q の3倍です。底面積が同じなので、円柱と円錐の体積の公式から3倍がすぐにわかります。このことより、立体 Q は 立体 P の4倍であるので、立体 P は立体 Q の 1 / 4 倍であるとも言うことができます。