ここでは、算数に関して3つのコラムを掲載しています。いろいろ思うことはありますが、諦めない気概を算数(数学?)で感じた瞬間でした。
- 不等号を知らない人が不等式の問題を解く
- 6÷2(1+2) = ? エクセル先生とマサオの回答
- 掛け算の順序問題
の3本です。サザエさん形式です。話に繋がりはありません。
スポンサーリンク
不等号を知らなくても何とか不等式の問題を解きたい
問題はできる範囲であきらめないで考え抜くことが大事です。答え方がわからなくても何とかしようとする気概が大切です。そんな根性を小学生に見せられました。では、その問題と回答です。
問題
時速 5 キロメートルで a キロメートル歩いたら、2時間未満だった。これを式を使って表しなさい。
回答
模範回答は、a / 5 < 2 です。
だが小学生は不等号など知りません。それでも、何とか自分の知識の範囲で回答を考え抜きました。それが、
a ÷ 5 = 2時間未満
です。
見事というしかありません。脱帽です。知らない記号(<)は言葉で補っています。きっと大物になることでしょう。
6÷2(1+2) = ?
この問題は2つの派閥に分かれます。答えが9であると主張する派閥と1であるという派閥です。
9であるとの主張
6÷2(1+2)
= 6÷2×(1+2) ← 掛けるが登場します
= 6÷2×3
= 3×3
= 9
1であるとの主張
6÷2(1+2)
= 6÷{2×(1+2)} ← 掛けると括弧が追加されます
= 6÷(2×3)
= 6÷6
= 1
争点
争点は、2(1+2) の扱いをどうするかです。正直なところ問題が悪すぎるので、結論は正直どちらでも良いのですが、スッキリしないのでエクセル先生はどのように考えるのかを聞いてみることにしました。以下がその結果です。
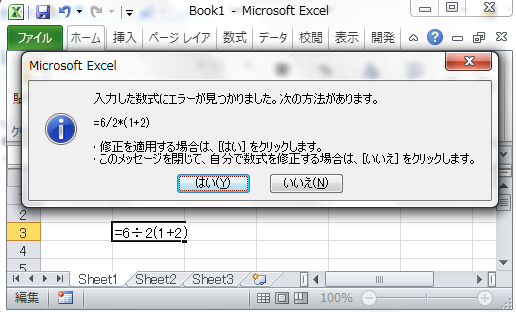
エクセル先生の回答 入力した数式にエラーが見つかりました。
入力が間違ってると指摘して、答えが9となる式を候補にあげてきました。ただ、エクセル先生は入力ミスを指摘しているだけなので、答えがどのようになるかはわかりません。
当然と言えば当然です。繰り返しになりますが、そもそも問題が悪すぎです。
マサオの見解
一応ここまで見てきたマサオの見解です。わたしは、答えが1になる派閥でしょうか?
式 6÷2(1+2) において、A = (1+2) とおきます。
6÷2(1+2) = 6÷2A = 3÷A =3÷(1+2) = 1
です。ただし、しつこく繰り返しますが、それがどうしたという感じです。では、次の話題にいきます。
小学生 掛け算の順序問題
個人的にはバカバカしい話だと思っています。例えば、「全部のお皿にはりんごが3個ずつあります。お皿は全部で4皿あります。全部で何個?」という問題で、3 × 4 = 12 なら正解で、4 × 3 = 12 は不正解といった具合です。(正解・不正解は逆かもしれません。どうでもいいことです)
小学校の先生は何も思わないのでしょうか?まさかドヤ顔して教えている先生はいないですよね?
これは長方形の面積を求める問題で、学校では、縦 × 横 で面積の求め方を教えているから、縦が先に書いてないと不正解とするようなものです。( 横 × 縦 で途中の計算したら不正解だZ (´◉◞౪◟◉) )
お話になりません。
学校では、掛け算の順序云々で間違った無意味なことを教えるくらいであれば、どちらでも答えは一緒になると言うことを教えるようにしたほうが良いと思います。例え正しく理解できなくてもです。クダラナイ屁理屈教えるよりはよっぽどマシです。
ちなみに、先生が時間を掛けて教えた間違いを正すのは、何年生でしょうか?