ここでは、高校生で履修する分数関数についての概要とポイントの整理を行っています。受験生の皆さん、最後の追い込みです。気を抜かずに頑張りましょう。ただし、体調管理は最優先です。無理は控えましょう。
スポンサーリンク
分数関数
x の関数 y が、y = 1 / x や y = (2x -3) / (3x -5) のような x の分数式で芦原されるとき、y を x の分数関数と言います。
分数関数では分母が 0 となるような x の値に対して y は定義されませんので、分数関数の定義域は、分母を 0 にしない実数を扱います。
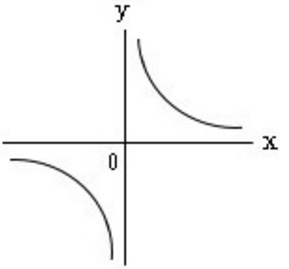
y = k / x
中学生で反比例を表す関数として習ったと思いますが、グラフにすると双曲線と呼ばれる曲線の一種で表されます。
双曲線上の点は、原点から遠ざかるにつれて一定の直線に限りなく近づいていきます。(が、悲しいことに交わることはありません。ロミオとジュリエットを思い出して涙です)
このような直線を双曲線の漸近線といいます。とくに、2つの漸近線が直行する双曲線を直角双曲線といいます。
y = k / (x – p) + q
y = k / (x – p) + q のグラフは、y = k / x のグラフを x 軸方向に p、y 軸方向に q だけ平行移動した直角双曲線となります。このとき、漸近線は、直線 x = p と直線 y = q です。
y = (ax + b) / (cx + d)
y = (ax + b) / (cx + d) ( c ≠ 0, ad ≠ bc ) は、分子を分母で割ることにより、y = k / (x – p) + q の形に変形することができます。よって、関数 y = (ax + b) / (cx + d) ( c ≠ 0, ad ≠ bc ) のグラフは、x 軸、y 軸に平行な漸近線をもつ直角双曲線となります。
ad = bc のときは、y = a / c となり、定数関数になります。