ここでは、円錐の表面積を求める方法を考えます。読み終えるころには新たな公式も誕生していることでしょう。
スポンサーリンク
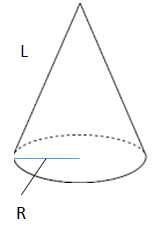
円錐とは、以下のように底面が円で、先がとんがった形です。これは知っていますよね。底面の半径をR、母線をLとしています。
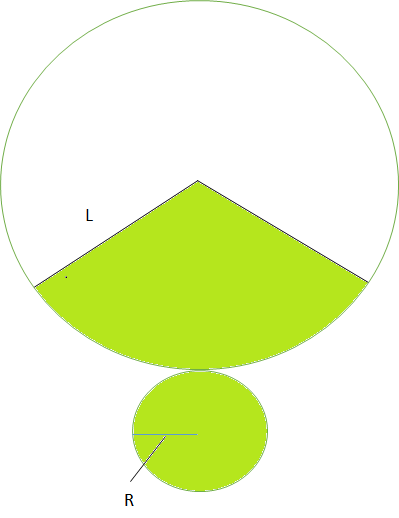
では、上記の円錐の表面積を求めてみたいと思います。面積を求めるには、円錐を下図のように展開します。色の付いた部分の面積が円錐の面積となります。扇形の面積と円の面積の合計ですね。
まずは、上記からわかることを整理してみましょう。
| 扇形の弧の長さ | 底面の円の円周と等しく、2Rπ |
| 大きな円(半径L)の円周 | 2Lπ |
| 大きな円(半径L)と扇形の面積比 | 2Lπ(半径Lの円の円周) : 2Rπ(扇形の弧の長さ) |
これらの情報を元に、扇形の表面積を求めて生きたいと思います。
扇形の面積 = 底面の円の面積 + 扇形の面積
= R × R × π + ( L × L × π ) × 2Rπ / 2Lπ
= R2 π + LRπ
これで、扇形の表面積を計算することができました。毎回このように計算してももちろんよいのですが、この計算結果から1つの公式を求めることができます。それは、
円錐の側面積 = LRπ
であるということです。このような公式が隠れていました。次回からはあっという間に計算できそうですね。
これで、計算が早くできるようになりますね
例題
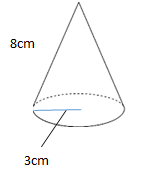
下記のような円錐の側面積を求めよ。
解答
円錐の側面積を求める公式より、
円錐の側面積 = 母線 × 半径 × 円周率
= 8cm × 3cm × π = 24 π cm2
扇形の面積を求める公式を導出する
円錐の側面積 = LRπ で求めることができることがわかりましたが、この式を変形してみます。
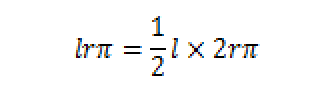
式を変形
小文字になってしまっていますが気にしないでください。理由はありあません。私のミスです。
ここで、2 r π は底面の直径であり、扇形の弧の長さです。つまり、扇形の弧の長さ ( L ) がわかれば、扇形の面積 ( S ) は、( 扇形の半径 ) × ( 扇形の弧の長さ ) / 2 で求めることができるということです。
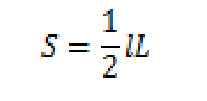
扇形の面積を求める公式