ここでは、中学数学で履修する三角形・四角形・台形の中点連結定理について掲載しています。
スポンサーリンク
中点連結定理 ( 三角形 )
下図のような、△ ABC の AB と AC の中点をそれぞれ M, N とするとき、MN // BC ( MN とBC は平行 ) かつ 2 × MN = BC ( MN の長さは BC の半分 ) となります。どのような三角形にもいえます。
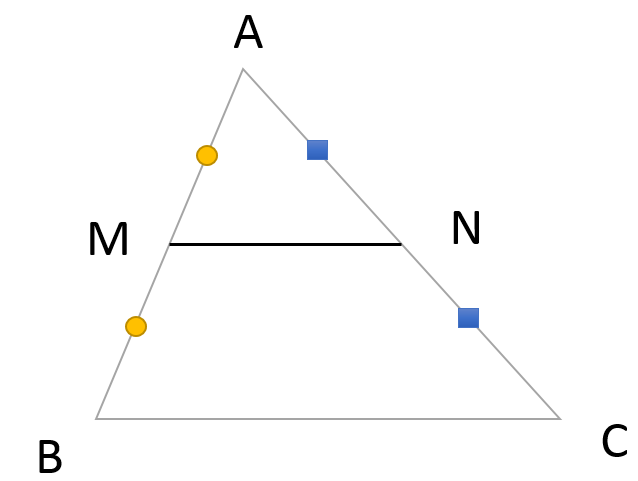
中点連結定理
証明
三角形の相似の証明から導きます。△ ABC と △ AMN について
∠Aは共通 ・・・①
AM:AN = AB:AC ・・・②
①、② より、2組の辺の比が等しくその間の角が等しいので △ ABC ∽ △ AMN
相似比は 2 : 1 です。よって、2 × MN = BC
また、△ ABC ∽ △ AMN なので、∠AMN = ∠ABC より MN // BC
∠AMN = ∠ABC ということは、MN と BC から見ると錯角が等しいと言うことになります。錯角が等しいということは平行であるということがいえます。
中点連結定理 ( 四角形 )
次に四角形の場合を考えて見ます。下図のように四角形ABCD の辺の中点を結んでできる四角形は平行四辺形になります。元の四角形が長方形や正方形の場合は、それぞれひし形と正方形になります。正方形も長方形も平行四辺形の1つの形態です。
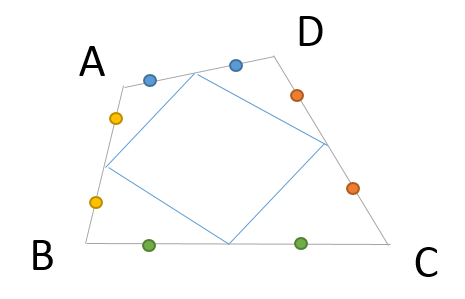
中の四角形は平行四辺形
上の図では平行四辺形に見えない?錯覚です。錯角だけに。うまい。
ただ、四角形の中点連結定理というものはありません。三角形の中点連結定理から導かれた結果です。AC と BD を結んで対角線をひくと、中点を結んだ三角形が4つ出現します。それぞれ、AC と BD と平行で長さも同じであることがわかります。自分で確認してみましょう。
中点連結定理 ( 台形 )
先に言っておきますと。これも台形だからというよりも三角形の中点連結定理からいえることであります。
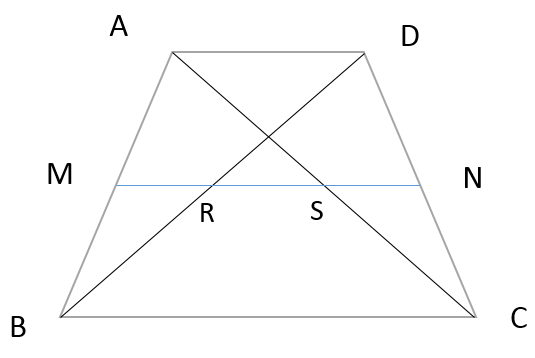
図のような台形の中点 M, N を結んだ線と対角線の交点を R, S とするとき、
- MN = ( AD + BC ) / 2
- RS = ( BC – AD ) / 2
であることがいえます。
証明 ( というよりは説明 )
△ ABC と △ ACD の2つを別々に見ると、MS = BC / 2, SM = AD / 2 であることが中点連結定理からわかります。MS + SM = MN なので、MN = BC / 2 + AD / 2 = ( AD + BC ) / 2 がわかります。
次に、△ ABC と △ ABD にそれぞれ着目します。MS = BC / 2 であり、MR = AD / 2 です。MS – MR = RS なので、RS = BC / 2 – AD / 2 = ( BC – AD ) / 2 であることがわかります。